
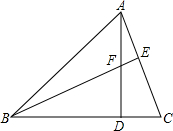
 如图,△ABC的两条高线AD,BE交于点F,∠BAD=45°,∠C=60°,则∠ABF的度数为15°.
如图,△ABC的两条高线AD,BE交于点F,∠BAD=45°,∠C=60°,则∠ABF的度数为15°.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
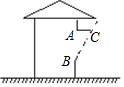 如图,某地夏季中午,当太阳移至房顶上方偏南时,光线与地面成80°角,房屋朝南的窗子高AB=1.8m,要在窗子外面上方安装水平挡光板AC,使午间光线不能直接射入室内,那么挡光板的宽度AC为( )
如图,某地夏季中午,当太阳移至房顶上方偏南时,光线与地面成80°角,房屋朝南的窗子高AB=1.8m,要在窗子外面上方安装水平挡光板AC,使午间光线不能直接射入室内,那么挡光板的宽度AC为( )| A. | 1.8tan80°m | B. | 1.8cos80°m | C. | $\frac{1.8}{sin80°}$ m | D. | $\frac{1.8}{tan80°}$ m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AD是高,CE是中线,点G是CE的中点,DG⊥CE,点G为垂足.
如图,△ABC中,AD是高,CE是中线,点G是CE的中点,DG⊥CE,点G为垂足.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
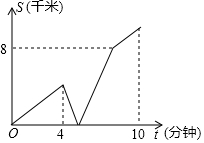 在一条笔直的公路上,依次有A、B、C三地.小军、小扬从A地同时出发匀速运动,小军以2千米/分的速度到达B地立即返回A地,到达A后小军原地休息,小扬途经B地前往C地.小军与小扬的距离s(单位:千米)和小扬所用的时间t(单位:分钟)之间的函数关系如图所示.下列说法:
在一条笔直的公路上,依次有A、B、C三地.小军、小扬从A地同时出发匀速运动,小军以2千米/分的速度到达B地立即返回A地,到达A后小军原地休息,小扬途经B地前往C地.小军与小扬的距离s(单位:千米)和小扬所用的时间t(单位:分钟)之间的函数关系如图所示.下列说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com