
【题目】如图,一次函数y=- ![]() x+b的图象与x轴、y轴分别交于点A、B,线段AB的中点为D(3,2).将△AOB沿直线CD折叠,使点A与点B重合,直线CD与x轴交于点C.
x+b的图象与x轴、y轴分别交于点A、B,线段AB的中点为D(3,2).将△AOB沿直线CD折叠,使点A与点B重合,直线CD与x轴交于点C.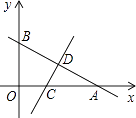
(1)求此一次函数的解析式;
(2)求点C的坐标;
(3)在坐标平面内存在点P(除点C外),使得以A、D、P为顶点的三角形与△ACD全等,请直接写出点P的坐标.
【答案】
(1)解:设A点坐标为(a,0),B点坐标为(0,b),
由线段AB的中点为D(3,2),得
![]() =3,
=3, ![]() =2,
=2,
解得a=6,b=4.
即A(6,0),B(0,4)
故一次函数解析式为y=- ![]() x+4
x+4
(2)解:如图1:
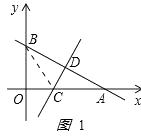
连接BC,设OC=x,则AC=CB=6-x,
∵∠BOA=90°,
∴OB2+OC2=CB2,
42+x2=(6-x)2,
解得x= ![]() ,
,
即C( ![]() ,0)
,0)
(3)解:①当△ACD≌△APD时,设P1(c,d),
由D是PC的中点,得
![]() ,
, ![]() =2,
=2,
解得c= ![]() ,d=4,
,d=4,
即P1( ![]() ,4);
,4);
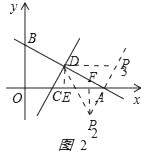
如图2:
 ,
,
②当△ACD≌△DP2A时,
做DE⊥AC与E,P2F⊥AC与F点,DE=2,CE= ![]() ,
,
由△CDE≌△AP2F,
AF=CE= ![]() ,P2F=DE=2,
,P2F=DE=2,
OF=6- ![]() =
= ![]() ,
,
∴P2( ![]() ,-2);
,-2);
③当△ACD≌△DP3A时,设P3(e,f)
A是线段P2P3的中点,得
![]() ,
, ![]() ,
,
解得e= ![]() ,f=2,
,f=2,
即P3( ![]() ,2),
,2),
综上所述:P1( ![]() ,4);P2(
,4);P2( ![]() ,-2);P3(
,-2);P3( ![]() ,2)
,2)
【解析】(1)把点D的坐标代入一次函数的解析式求出A,B的坐标和b的值,得到一次函数的解析式;(2)根据勾股定理求出点C的坐标;(3)根据题意和全等三角形的判定方法,求出各个点的坐标,得到点P的坐标;此题是综合题,难度较大,计算和解方程时需认真仔细.


科目:初中数学 来源: 题型:
【题目】如图.在Rt△ABC中,∠ABC=90°,点D是斜边上的中点,点P在AB上,PE⊥BD于E,PF⊥AC于F,若AB=6,BC=3,则PE+PF=( ) 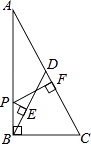
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝首个“中国农民丰收节”,海淀区将在海淀公园举办京西稻收割节活动,京西稻是著名农业作物,颗粒圆润,晶莹明亮,稻谷每粒重约0.000028千克.将0.000028用科学记数法表示为( )
A. 2.8×10﹣5B. 2.8×10﹣6C. 28×10﹣6D. 0.28×10﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
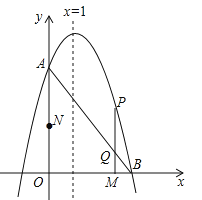
【题目】如图,已知抛物线![]() 与y轴相交于点A(0,3),与x正半轴相交于点B,对称轴是直线x=1.
与y轴相交于点A(0,3),与x正半轴相交于点B,对称轴是直线x=1.
(1)求此抛物线的解析式以及点B的坐标.
(2)动点M从点O出发,以每秒2个单位长度的速度沿x轴正方向运动,同时动点N从点O出发,以每秒3个单位长度的速度沿y轴正方向运动,当N点到达A点时,M、N同时停止运动.过动点M作x轴的垂线交线段AB于点Q,交抛物线于点P,设运动的时间为t秒.
①当t为何值时,四边形OMPN为矩形.
②当t>0时,△BOQ能否为等腰三角形?若能,求出t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知一次函数y=x﹣1的图象经过P1(x1 , y1)、P2(x2 , y2)两点,若x1<x2 , 则y1y2(填“>”,“<”或“=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC.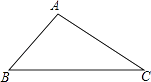
(1)利用直尺和圆规,按照下列要求作图(保留作图痕迹,不要求写作法)
①作∠ABC的平分线BD交AC于点D;
②作线段BD的垂直平分线分别交AB、BC于点E、F.
(2)连接DE,请判断线段DE与线段BF的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com