
【题目】观察下列等式:
第1个等式:![]()
第2个等式:![]()
第3等式:![]()
第4个等式:![]()
请解答下列问题:
(1)按以上规律写出第5个等式:a5= = .
(2)用含n的式子表示第n个等式:an= = (n为正整数).
(3)求a1+a2+a3+a4+…+a2018的值.
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
【题目】小林沿着笔直的公路靠右匀速行走,发现每隔5分钟从背后驶过一辆101路公交车,每隔3分钟从迎面驶来一辆101路公交车.假设每个每辆101路公交车行驶速度相同,而且101路公交车总站每隔固定时间发一辆车,那么发车间隔的时间是( )
A. 3分钟 B. 3.75分钟 C. 4分钟 D. 5分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,成绩被分别绘制成如下两个统计图:
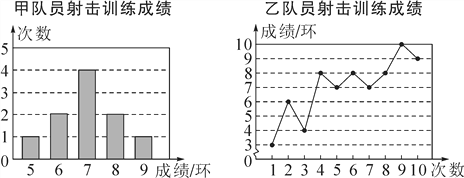
根据以上信息,整理分析数据如下:
平均成绩(环) | 中位数(环) | 众数(环) | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | 4.2 |
(1)则表格中a,b的值分别是a=________,b=________;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O在直径,AD,BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD,OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2 , ④OD:OC=DE:EC,⑤OD2=DECD,正确的有( ) 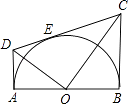
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A,O,B分别表示﹣15,0,9,点P,Q分别从点A,B同时开始沿数轴正方向运动,点P的速度是每秒3个单位,点Q的速度是每秒1个单位,运动时间为t秒.在运动过程中,若点P,Q,O三点其中一个点恰好是另外两点为端点的线段的一个三等分点,则运动时间为_____秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB是某天然气公司的主输气管道,点C、D是在AB异侧的两个小区,现在主输气管道上寻找支管道连接点,向两个小区铺设管道。有以下两个方案:
方案一:只取一个连接点P,使得像两个小区铺设的支管道总长度最短,在图中标出点P的位置,保留画图痕迹;
方案二:取两个连接点M和N,使得点M到C小区铺设的支管道最短,使得点N到D小区铺设的管道最短. 在途中标出M、N的位置,保留画图痕迹;
设方案一中铺设的支管道总长度为L1,方案二中铺设的支管道总长度为L2,则L1与L2的大小关系为:L1_______L2(填“>”、“<”或“=”)理由是____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,b满足![]() +(c-7)2=0.
+(c-7)2=0.
(1) a= ,b= ,c= .
(2) 若将数轴折叠,使得A点与C点重合,则点B与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= ,BC= .(用含t的代数式表示)
(4) 请问:3BC-2AB的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=60°
(1)如图1,点E为线段AB的中点,连接DE、CE,若AB=4,求线段EC的长;
(2)如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论.
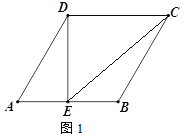
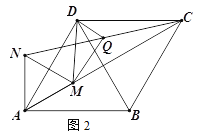
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com