
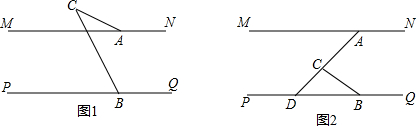
分析 (1)作CE∥PQ,根据平行线的性质以及角的和差关系进行推导即可;
(2)①根据三角形外角性质,即可得到∠ADB=∠SAC+∠ASQ,∠ACB=∠ADB+∠PBC,进而得出∠ACB=∠SAC+∠ASQ+∠PBC;
②根据三角形内角和定理,即可得到∠ACB+∠SAC=180°-∠AEC,∠PBC+∠ASQ=180°-∠BES,再根据对顶角相等,即可得到∠ACB+∠SAC=∠PBC+∠ASQ.
解答 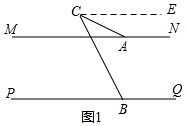 解:(1)如图1,作CE∥PQ,
解:(1)如图1,作CE∥PQ,
∵CE∥PQ,MN∥PQ,
∴CE∥MN,
∴∠CAM=∠ACE,∠CBP=∠BCE,
∴∠CBP-∠CAM=∠BCE-∠ACE=∠C;
(2)①当点S在点D的左边时,∠SAC+∠ASQ+∠PBC=∠ACB.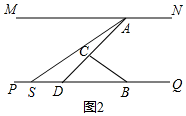
证明:如图2,∵∠ADB是△ADS的外角,
∴∠ADB=∠SAC+∠ASQ,
∵∠ACB是△BCD的外角,
∴∠ACB=∠ADB+∠PBC,
∴∠ACB=∠SAC+∠ASQ+∠PBC;
②如右图,当点S在点D的右边时,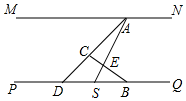
∵∠ACB+∠SAC=180°-∠AEC,∠PBC+∠ASQ=180°-∠BES,
又∵∠AEC=∠BES,
∴∠ACB+∠SAC=∠PBC+∠ASQ,
即∠SAC,∠PBC,∠ACB,∠ASQ之间的数量关系为∠ACB+∠SAC=∠PBC+∠ASQ.
故答案为:∠ACB+∠SAC=∠PBC+∠ASQ.
点评 本题主要考查了平行线的性质,三角形外角性质以及三角形内角和定理的综合应用,解题时注意:两直线平行,内错角相等.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
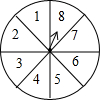 如图,转盘被平均分成8个区域,每个区域分别标注数字1、2、3、4、5、6、7、8,任意转动转盘一次,规定:如果指针恰好指在分割线上,那么重转一次,直到指针指向一个标有数字的区域为止.写出下列事件发生的概率:
如图,转盘被平均分成8个区域,每个区域分别标注数字1、2、3、4、5、6、7、8,任意转动转盘一次,规定:如果指针恰好指在分割线上,那么重转一次,直到指针指向一个标有数字的区域为止.写出下列事件发生的概率:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有这样一个问题:探究函数y=$\frac{1}{x}$+1的图象与性质.
有这样一个问题:探究函数y=$\frac{1}{x}$+1的图象与性质.| x | … | -4 | -3 | -2 | -1 | -m | m | 1 | 2 | 3 | 4 | … |
| y | … | $\frac{3}{4}$ | $\frac{2}{3}$ | $\frac{1}{2}$ | 0 | -1 | 3 | 2 | $\frac{3}{2}$ | $\frac{4}{3}$ | $\frac{5}{4}$ | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com