
【题目】已知:抛物线 ![]() 与
与 ![]() 轴分别交于点A(-3,0),B(m,0).将y1向右平移4个单位得到y2 .
轴分别交于点A(-3,0),B(m,0).将y1向右平移4个单位得到y2 .
(1)求b的值;
(2)求抛物线y2的表达式;
(3)抛物线y2与 ![]() 轴交于点D,与
轴交于点D,与 ![]() 轴交于点E、F(点E在点F的左侧),记抛物线在D、F之间的部分为图象G(包含D、F两点),若直线
轴交于点E、F(点E在点F的左侧),记抛物线在D、F之间的部分为图象G(包含D、F两点),若直线 ![]() 与图象G有一个公共点,请结合函数图象,求直线
与图象G有一个公共点,请结合函数图象,求直线 ![]() 与抛物线y2的对称轴交点的纵坐标t的值或取值范围.
与抛物线y2的对称轴交点的纵坐标t的值或取值范围.
【答案】
(1)解:把A(-3,0)代入y1=x2+bx+3得:9-3b+3=0,
解得:b=4,
∴y1的表达式为:y=x2+4x+3
(2)解:将y1变形得:y1=(x+2)2-1
据题意y2=(x+2-4)2-1=(x-2)2-1=x2-4x+3;
∴抛物线y2的表达式为y=x2-4x+3
(3)解:∵y2=(x-2)2-1,函数图像如图所示:

∴对称轴是x=2,顶点为(2,-1);
当y2=0时,x=1或x=3,
∴E(1,0),F(3,0),D(0,3),
∵直线y=kx+k-1过定点(-1,-1),
当直线y=kx+k-1与图象G有一个公共点时,t=-1,
当直线y=kx+k-1过F(3,0)时,3k+k-1=0,
解得:k= ![]() ,
,
∴直线解析式为y= ![]() x-
x- ![]() ,
,
把x=2代入= ![]() x-
x- ![]() ,得:y=-
,得:y=- ![]() ,
,
当直线过D(0,3)时,k-1=3,
解得:k=4,
∴直线解析式为y=4x+3,
把x=2代入y=4x+3得:y=11,即t=11,
∴结合图象可知t=-1,或 ![]() <t≤11.
<t≤11.
【解析】(1)把点A的坐标代入可求出b的值,即可得到函数解析式;
(2)先把y1的解析式化成顶点式,再根据平移规律可求出;
(3)画出函数y2的图象,可求出此函数与x轴、y轴的交点坐标;直线y=kx+k-1过定点(-1,-1),再根据直线y=kx+k-1与图象G有一个公共点可求出t=-1;再由直线y=kx+k-1过F(3,0)和过D(0,3),分别求出此直线的解析式,从而得出t的值,再结合图像进而可得出答案.
【考点精析】掌握二次函数图象的平移和抛物线与坐标轴的交点是解答本题的根本,需要知道平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距_____千米.
(2)走了一段路后,自行车发生故障进行修理,所用的时间是____小时.
(3)B出发后_____小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.(写出计算过程)
(5)请通过计算说明:若B的自行车不发生故障,保持出发时的速度前进,何时与A相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚在实践课上要做一个如图1所示的折扇,折扇扇面的宽度AB是骨柄长OA的 ![]() ,折扇张开的角度为120°.小刚现要在如图2所示的矩形布料上剪下扇面,且扇面不能拼接,已知矩形布料长为24
,折扇张开的角度为120°.小刚现要在如图2所示的矩形布料上剪下扇面,且扇面不能拼接,已知矩形布料长为24 ![]() cm,宽为21cm.小刚经过画图、计算,在矩形布料上裁剪下了最大的扇面,若不计裁剪和粘贴时的损耗,此时扇面的宽度AB为( )
cm,宽为21cm.小刚经过画图、计算,在矩形布料上裁剪下了最大的扇面,若不计裁剪和粘贴时的损耗,此时扇面的宽度AB为( )
A.21cm
B.20 cm
C.19cm
D.18cm
查看答案和解析>>
科目:初中数学 来源: 题型:
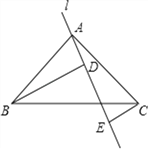
【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,直线l为经过点A的任一直线,BD⊥l于D,CE⊥AE,若BD>CE,试问:
(1)AD与CE的大小关系如何?请说明理由;
(2)线段BD,DE,CE之间的数量之间关系如何?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司要把一台机器运往外地,现有两种运输方式可供选择;
方式一:使用快递公司运输,装卸费![]() 元,另外每千米再加收
元,另外每千米再加收![]() 元;
元;
方式二:使用货车运输,装卸费![]() 元,另外每千米再加收
元,另外每千米再加收![]() 元.
元.
(1)若运输路程是![]() 千米,请用含
千米,请用含![]() 的代数式分别表示两种运输方式的总费用;
的代数式分别表示两种运输方式的总费用;
(2)若两种运输方式的总费用相同,求运输这台机器的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线 ![]() 与x轴交于点A(-2,0)、B(4,0)两点,与y轴交于点C.
与x轴交于点A(-2,0)、B(4,0)两点,与y轴交于点C.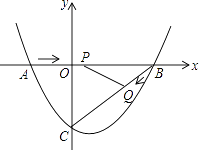
(1)求抛物线的表达式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度向C点运动.其中一个点到达终点时,另一个点也停止运动.当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使 ![]() ,求K点坐标.
,求K点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
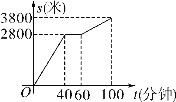
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列四种说法:①小明中途休息用了20分钟;②小明休息前爬山的平均速度为每分钟70米;③小明在上述过程中所走的路程为6600米;④小明休息前爬山的平均速度大于休息后爬山的平均速度.其中正确的是________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)探究:哪些特殊的角可以用一副三角板画出?
在①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,小明同学利用一副三角板画不出来的特殊角是_________;(填序号)
中,小明同学利用一副三角板画不出来的特殊角是_________;(填序号)
(2)在探究过程中,爱动脑筋的小明想起了图形的运动方式有多种.如图,他先用三角板画出了直线![]() ,然后将一副三角板拼接在一起,其中
,然后将一副三角板拼接在一起,其中![]() 角(
角(![]() )的顶点与
)的顶点与![]() 角(
角(![]() )的顶点互相重合,且边
)的顶点互相重合,且边![]() 、
、![]() 都在直线
都在直线![]() 上.固定三角板
上.固定三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 按顺时针方向旋转一个角度
按顺时针方向旋转一个角度![]() ,当边
,当边![]() 与射线
与射线![]() 第一次重合时停止.
第一次重合时停止.

①当![]() 平分
平分![]() 时,求旋转角度
时,求旋转角度![]() ;
;
②是否存在![]() ?若存在,求旋转角度
?若存在,求旋转角度![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以等腰直角三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1……如此作下去,若OA=OB=1.
(1)A1B=________,S△A1B1A2=________;
(2)试猜想第n个等腰直角三角形的面积Sn.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com