
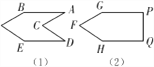
【题目】如图是小明设计的智力拼图玩具,现在小明遇到了下面两个问题,请你帮助解决.
(1)如图⑴,∠D=![]() ,∠ACD=
,∠ACD=![]() .为保证AB∥DE,∠A应等于多少度?
.为保证AB∥DE,∠A应等于多少度?
(2)如图⑵,若GP∥HQ,则∠G,∠F, ∠H之间有什么样的关系?
【答案】(1)∠A=![]() ;(2)∠G+ ∠F+∠H=
;(2)∠G+ ∠F+∠H=![]()
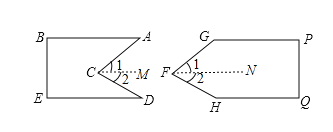
【解析】试题分析:(1)过C作CM∥AB,根据平行线的性质可得∠A=∠1=28°,再计算∠2=∠D=32°可得答案;
(2)当∠G+∠GFH+∠H=360°时,GP∥HQ;过F作FN∥GP,然后证明∠2+∠H=180°进而可得FN∥HQ,从而可证出GP∥HQ.
试题解析:
(1)∠A=28°;
如图所示:过C作CM∥AB,
∴∠A=∠1=28°,
∵∠ACD=60°,
∴∠2=32°,
∵∠D=32°,
∴CM∥ED,
∵AB∥CM,
∴AB∥DE;
(2)当∠G+∠GFH+∠H=360°时,GP∥HQ;理由如下:
如图所示:过F作FN∥GP,
∴∠G+∠1=180°,
∵∠G+∠1+∠2+∠H=360°,
∴∠2+∠H=180°,
∴FN∥HQ,
∵GP∥HQ,
∴GP∥HQ.


科目:初中数学 来源: 题型:
【题目】下列事件中,不可能事件是( )
A. 今年的除夕夜会下雪
B. 在只装有红球的袋子里摸出一个黑球
C. 射击运动员射击一次,命中10环
D. 任意掷一枚硬币,正面朝上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
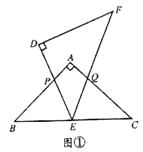
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
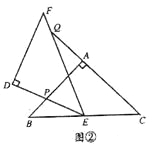
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP= ![]() ,CQ=
,CQ= ![]() 时,P、Q两点间的距离 (用含
时,P、Q两点间的距离 (用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程(k-1)x2+2kx+2=0
(1)(4分)求证:无论k为何值,方程总有实数根。
(2)(5分)设x1,x2是方程(k-1)x2+2kx+2=0的两个根,记S=![]() +
+![]() + x1+x2,S的值能为2吗?若能,求出此时k的值。若不能,请说明理由。
+ x1+x2,S的值能为2吗?若能,求出此时k的值。若不能,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;
![]()
(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的![]() ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,设△ABC的面积为S,周长为l.
(1)填表:
三边a、b、c |
|
|
3、4、5 | 2 | |
5、12、13 | 4 | |
8、15、17 | 6 |
(2)如果![]() ,观察上表猜想:
,观察上表猜想: ![]() (用含有m的代数式表示).
(用含有m的代数式表示).
(3)证明(2)中的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com