
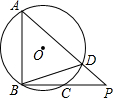 如图,点A,B,C,D在⊙O上,$\widehat{AB}$=2$\widehat{BC}$,$\widehat{AD}$=3$\widehat{BC}$,延长BC,AD交于点P,若∠CBD=18°,则∠P的大小为54°.
如图,点A,B,C,D在⊙O上,$\widehat{AB}$=2$\widehat{BC}$,$\widehat{AD}$=3$\widehat{BC}$,延长BC,AD交于点P,若∠CBD=18°,则∠P的大小为54°. 分析 连接AC,根据圆周角定理得到∠CAD=∠CBD=18°,设∠BAC=x,根据三角形的内角和列方程得到∠BAD=45°,∠ABC=81°,于是得到结论.
解答 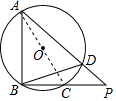 解:连接AC,
解:连接AC,
∴∠CAD=∠CBD=18°,
设∠BAC=x,
∵$\widehat{AB}$=2$\widehat{BC}$,$\widehat{AD}$=3$\widehat{BC}$,
∴∠ABD=2∠BAC,∠ADB=2∠BAC,
∴∠ABD=3x,∠ADB=2x,
∴x+2x+3x+18°=180°,
∴x=27°,
∴∠BAD=45°,∠ABC=81°,
∴∠P=180°-45°-81°=54°,
故答案为:54°.
点评 本题考查了圆周角定理,三角形的内角和定理,熟练掌握三角形的内角和定理是解题的关键.


科目:初中数学 来源: 题型:填空题
 如图,点P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC,PF⊥CD,垂足分别为点E、F,连接EF,下列结论①△FPD是等腰直角三角形;②AP=EF;③AD=PD;④∠PFE=∠BAP,其中正确的结论是①②④(请填序号)
如图,点P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC,PF⊥CD,垂足分别为点E、F,连接EF,下列结论①△FPD是等腰直角三角形;②AP=EF;③AD=PD;④∠PFE=∠BAP,其中正确的结论是①②④(请填序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
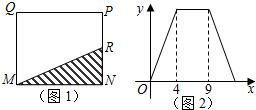 如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停下,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )
如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停下,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )| A. | 当x=2时,y=5 | B. | 矩形MNPQ的面积是20 | ||
| C. | 当x=6时,y=10 | D. | 当y=$\frac{15}{2}$时,x=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
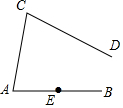 如图,已知∠ACD=75°,点E在AB上.
如图,已知∠ACD=75°,点E在AB上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
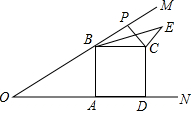 如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为2$\sqrt{3}$+2.
如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为2$\sqrt{3}$+2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com