
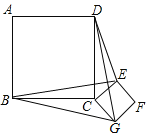
【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+b2,其中正确结论是_____(填序号)
【答案】①②
【解析】
由四边形ABCD与四边形EFGC都为正方形,得到四条边相等,四个角为直角,利用SAS得到三角形BCE与三角形DCG全等,利用全等三角形对应边相等即可得到BE=DG,利用全等三角形对应角相等得到∠1=∠2,利用等角的余角相等及直角的定义得到∠BOD为直角,利用勾股定理求出所求式子的值即可.
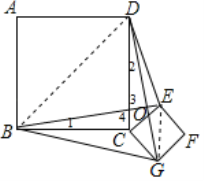
如图,设BE,DG交于O,
∵四边形ABCD和EFGC都为正方形,
∴BC=CD,CE=CG,∠BCD=∠ECG=90°,
∴∠BCE+∠DCE=∠ECG+∠DCE=90°+∠DCE,即∠BCE=∠DCG,
在△BCE和△DCG中,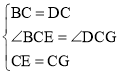 ,
,
∴△BCE≌△DCG(SAS),
∴∠1=∠2,BE=DG,故①正确,
∵∠3=∠4,∠BCD=90°,
∴∠1+∠4=∠3+∠2=90°,
∴∠BOD=90°,
∴BE⊥DG;故②正确;
如图,连接BD,EG,
∴DO2+BO2=BD2=BC2+CD2=2a2,EO2+OG2=EG2=CG2+CE2=2b2,
∴BG2+DE2=OG2+BO2+EO2+ DO2=2a2+2b2,故③错误.
故答案为:①②.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
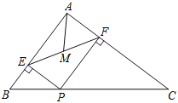
【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,城市建设部门计划在城市广场的一块长方形空地上修建一个面积为1500![]() 的停车场,将停车场四周余下的空地修建成同样宽的通道,已知长方形空地的长为60
的停车场,将停车场四周余下的空地修建成同样宽的通道,已知长方形空地的长为60![]() ,宽为40
,宽为40![]() .
.

(1)求通道的宽度;
(2)某公司希望用60万元的承包金额承揽修建广场的工程,城建部门认为金额太高需要降价,通过两次协商,最终以48.6万元达成一致,若两次降价的百分率相同,求每次降价的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
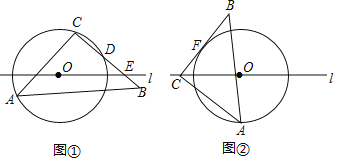
【题目】已知,△ABC中,∠ACB=90°,AC=BC=8,点A在半径为5的⊙O上,点O在直线l上.
(1)如图①,若⊙O经过点C,交BC于点D,求CD的长.
(2)在(1)的条件下,若BC边交l于点E,OE=2![]() ,求BE的长.
,求BE的长.
(3)如图②,若直线l还经过点C,BC是⊙O 的切线,F为切点,则CF的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
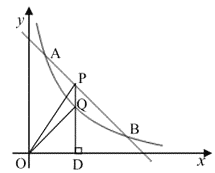
【题目】如图,一次函数y=kx+b与反比例函数![]() (x>0)的图象交于点A(a,3)和B(3,1).
(x>0)的图象交于点A(a,3)和B(3,1).
(1)求一次函数的解析式.
(2)观察图象,写出反比例函数值小于一次函数值时x的取值范围.
(3)点P是线段AB上一点,过点P作PD⊥x轴于点D,交反比例函数图象于点Q,连接OP、OQ,若△POQ的面积为![]() ,求P点的坐标。
,求P点的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,设运动的时间为ts,四边形APQC的面积为ymm2.

(1)y与t之间的函数关系式;
(2)求自变量t的取值范围;
(3)四边形APQC的面积能否等于172mm2.若能,求出运动的时间;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
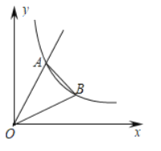
【题目】如图,正比例函数y1=k1x的图象与反比例函数y2=![]() (x>0)的图象相交于点A(
(x>0)的图象相交于点A(![]() ,2
,2![]() ),点B是反比例函数图象上一点,它的横坐标是3,连接OB,AB,则△AOB的面积是_____.
),点B是反比例函数图象上一点,它的横坐标是3,连接OB,AB,则△AOB的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
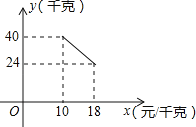
【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得150元的销售利润,销售价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com