
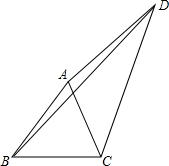
 如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,则CD=4.
如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,则CD=4. 分析 以CD为边向外作出等边三角形DCE,连接AE,得到∠ADE=90°,根据全等三角形的性质得到BD=AE=5,根据勾股定理即可得到结论.
解答 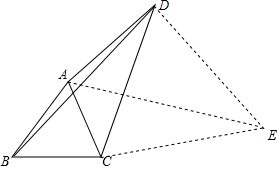 解:以CD为边向外作出等边三角形DCE,连接AE,
解:以CD为边向外作出等边三角形DCE,连接AE,
∵∠ADC=30°,
∴∠ADE=90°,
在△ACE与△BCD中$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{CE=DC}\end{array}\right.$,
∴△ACE≌△BCD,
∴BD=AE=5,
∴AD2+DE2=AE2,
∴33+DE2=52,
∴DE=CD=4.
故答案为:4.
点评 本题考查了全等三角形的性质,等边三角形的性质,勾股定理正确的作出辅助线是解题的关键.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:选择题
| A. | x10÷(x4÷x2)=x8 | B. | (xy)5÷(xy)3=xy2 | ||
| C. | 2xn+2÷xn+1=x2 | D. | (6x3-3x2+3x)÷(3x)=2x2-x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 测量体校篮球队和排球队中180名队员的身高 | |
| B. | 随机抽取本市一所学校的180名学生的身高 | |
| C. | 查阅有关外地180名学生身高的统计资料 | |
| D. | 在本地的市区和郊县各任选一所完全中学、两所初级中学,在这六所学校的七、八、九年级的一个班中,用抽签的方法分别选出10名学生,然后测量他们的身高. |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
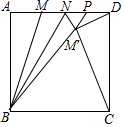 如图,正方形ABCD的边长为6,AM=$\frac{1}{3}$AD,点N在线段MD上,连接BN,把△BMN沿BN翻折,得到△BM′N,延长BM′交线段DN于点P,连接CM′,DM′,当△CDM′是等腰三角形时,MN的长为$\frac{131-24\sqrt{65}}{8}$或=$\frac{19\sqrt{31}+16}{54}$.
如图,正方形ABCD的边长为6,AM=$\frac{1}{3}$AD,点N在线段MD上,连接BN,把△BMN沿BN翻折,得到△BM′N,延长BM′交线段DN于点P,连接CM′,DM′,当△CDM′是等腰三角形时,MN的长为$\frac{131-24\sqrt{65}}{8}$或=$\frac{19\sqrt{31}+16}{54}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com