
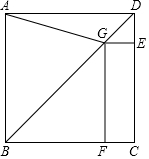
 如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.
如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.分析 (1)结论:AG2=GE2+GF2.只要证明GA=GC,四边形EGFC是矩形,推出GE=CF,在Rt△GFC中,利用勾股定理即可证明;
(2)过点A作AH⊥BG,在Rt△ABH、Rt△AHG中,求出AH、HG即可解决问题.
解答 解:(1)结论:AG2=GE2+GF2.
理由:连接CG.
∵四边形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形EGFC是矩形,
∴CF=GE,
在Rt△GFC中,∵CG2=GF2+CF2,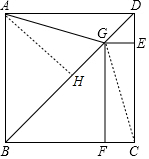
∴AG2=GF2+GE2.
(2)过点A作AH⊥BG,
∵四边形ABCD是正方形,
∴∠ABD=∠GBF=45°,
∵GF⊥BC,
∴∠BGF=45°,
∵∠AGF=105°,
∴∠AGB=∠AGF-∠BGF=105°-45°=60°,
在Rt△ABH中,∵AB=1,
∴AH=BH=$\frac{\sqrt{2}}{2}$,
在Rt△AGH中,∵AH=$\frac{\sqrt{2}}{2}$,∠GAH=30°,
∴HG=AH•tan30°=$\frac{\sqrt{6}}{6}$,
∴BG=BH+HG=$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{6}}{6}$.
点评 本题考查正方形的性质、矩形的判定和性质、勾股定理直角三角形30度的性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
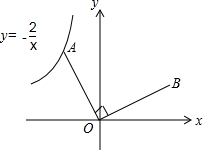 如图,已知点A是反比例函数y=-$\frac{2}{x}$的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为y=$\frac{2}{x}$.
如图,已知点A是反比例函数y=-$\frac{2}{x}$的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为y=$\frac{2}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
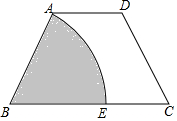 如图,四边形ABCD中,AB=CD,AD∥BC,以点B为圆心,BA为半径的圆弧与BC交于点E,四边形AECD是平行四边形,AB=6,则扇形(图中阴影部分)的面积是6π.
如图,四边形ABCD中,AB=CD,AD∥BC,以点B为圆心,BA为半径的圆弧与BC交于点E,四边形AECD是平行四边形,AB=6,则扇形(图中阴影部分)的面积是6π.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
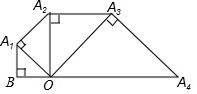 如图,已知OB=1,以OB为直角边作等腰直角三角形A1BO,再以OA1为直角边作等腰直角三角形A2A1O,如此下去,则线段OAn的长度为($\sqrt{2}$)n.
如图,已知OB=1,以OB为直角边作等腰直角三角形A1BO,再以OA1为直角边作等腰直角三角形A2A1O,如此下去,则线段OAn的长度为($\sqrt{2}$)n.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com