
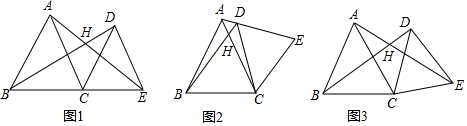
分析 (1)先判断出∠BCD=∠ACE,进而得出△BCD≌△ACE,即可得出BD=AE,∠CBD=∠CAE最后用三角形的内角和得出∠AHB=60°,
(2)作出辅助线,利用勾股定理即可计算得出结论;
(3)先判断出点A,C,E在同一条直线时,△ABH与△DHE面积之和的最大值,最大值是△ABC和△CDE面积之和.
解答 解:(1)∵△ABC,CDE都是等边三角形,
∴BC=AC,CD=CE,∠ACB=∠DCE=60°,
∴∠BCD=∠ACE,
在△BCD和△ACE中,$\left\{\begin{array}{l}{BC=AC}\\{∠BCD=∠ACE}\\{CD=CE}\end{array}\right.$,
∴△BCD≌△ACE,
∴BD=AE,∠CBD=∠CAE,
∵∠ABC+∠CBD=60°,
∴∠BAE+∠ABD=∠BAC+∠ABD+∠CAE=120°,
∴∠AHB=60°;
(2)如图2, 同(1)的方法得出,BD=AE,
同(1)的方法得出,BD=AE,
过点C作CF⊥AE,
∵△CDE是边长为2$\sqrt{3}$的等边三角形,
∴EF=$\sqrt{3}$,CF=3,
在Rt△ACF中,AC=4,CF=3,
∴AF=$\sqrt{A{C}^{2}-C{F}^{2}}$=$\sqrt{7}$,
∴BD=AE=AF+EF=$\sqrt{7}$+$\sqrt{3}$,
(3)如图3,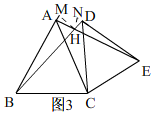 过点H作HM⊥AB,HN⊥DE,
过点H作HM⊥AB,HN⊥DE,
∴S△ABH=$\frac{1}{2}$AB×MH=2MH,S△DEH=$\frac{1}{2}$DE×HN=$\sqrt{3}$HN,
∴S△ABH+S△DEH=2MH+$\sqrt{3}$HN,
∴△CDE在运动过程中,点H和点C重合时,S△ABH+S△DEH最大,
即:点A,C,E在同一条直线上,
此时,S△ABH+S△DEH=S△ABC+S△CDE=$\frac{\sqrt{3}}{4}$AB2+$\frac{\sqrt{3}}{4}$DE2=4$\sqrt{3}$+3$\sqrt{3}$=7$\sqrt{3}$.
即:△ABH与△DHE面积之和的最大值为7$\sqrt{3}$.
点评 此题是几何变换综合题,主要考查了等边三角形的性质,全等三角形的判定和性质,勾股定理,极值问题,判断出BD=AE是解本题的关键,难点是点A,C,E在同一直线上时△ABH与△DHE面积之和最大.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:解答题
 【背景介绍】勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.
【背景介绍】勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
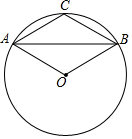 如图,已知AB为⊙O的弦长,且AB:AO=$\sqrt{3}$,点C为$\widehat{AB}$的中点,试猜想四边形AOBC的形状,并说明理由.
如图,已知AB为⊙O的弦长,且AB:AO=$\sqrt{3}$,点C为$\widehat{AB}$的中点,试猜想四边形AOBC的形状,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线l与x轴、y轴分别交于点A、点B,点A的坐标为(3,0),且∠OAB=30°,点C为线段AB上一动点,过点C作CD⊥x轴,垂足为点D.
如图,在平面直角坐标系中,直线l与x轴、y轴分别交于点A、点B,点A的坐标为(3,0),且∠OAB=30°,点C为线段AB上一动点,过点C作CD⊥x轴,垂足为点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 等腰Rt△ABC中,∠BAC=90°,AB=AC,点A、C分别在y轴、x轴上且点A,点C的坐标分别为A(0,a),C(b,0),满足a2+b2-4a-10b+29=0.
等腰Rt△ABC中,∠BAC=90°,AB=AC,点A、C分别在y轴、x轴上且点A,点C的坐标分别为A(0,a),C(b,0),满足a2+b2-4a-10b+29=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
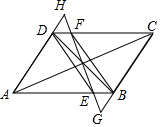 如图,已知?ABCD的对角线AC与BD相交于点O,过点O的直线与AB,DC分别交于点E,F
如图,已知?ABCD的对角线AC与BD相交于点O,过点O的直线与AB,DC分别交于点E,F查看答案和解析>>
科目:初中数学 来源: 题型:解答题
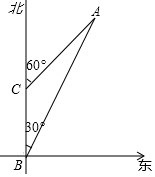 已知海岛A的周围6km的范围内有暗礁,一艘海轮在B处测得海岛A在北偏东30°的方向;向正北方向航行6km到达C处,又测得该岛在北偏东60°的方向,如果海轮不改变航向,继续向正北航行,有没有触礁的危险?
已知海岛A的周围6km的范围内有暗礁,一艘海轮在B处测得海岛A在北偏东30°的方向;向正北方向航行6km到达C处,又测得该岛在北偏东60°的方向,如果海轮不改变航向,继续向正北航行,有没有触礁的危险?查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省盐城市盐都区西片七年级下学期第一次月考数学试卷(解析版) 题型:单选题
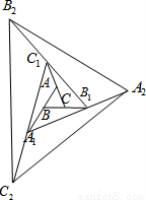
如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2017,最少经过( )次操作.
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com