

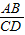 ≠1,而现在在不确定AB与CD的大小关系的时候是不能判断“四边形ABDC一定是梯形”.
≠1,而现在在不确定AB与CD的大小关系的时候是不能判断“四边形ABDC一定是梯形”.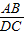 =
=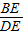 ,
,
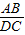 =
=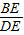 =1时,AB=CD,
=1时,AB=CD,

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 已知:如图,AD和BC相交于E点,∠EAB=∠ECD.
已知:如图,AD和BC相交于E点,∠EAB=∠ECD.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图Rt△ABD和Rt△BCD如图放置,∠BAD=∠BCD=90°,连接AC,若AC平分∠DAB,则线段AB、AD、AC有怎样的数量关系?写出你的猜想,并证明.
已知:如图Rt△ABD和Rt△BCD如图放置,∠BAD=∠BCD=90°,连接AC,若AC平分∠DAB,则线段AB、AD、AC有怎样的数量关系?写出你的猜想,并证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,AD和BC相交于E点,∠EAB=∠ECD.
已知:如图,AD和BC相交于E点,∠EAB=∠ECD.查看答案和解析>>
科目:初中数学 来源:福建省期末题 题型:解答题
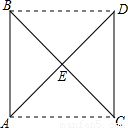
已知:如图,AD和BC相交于E点,∠EAB=∠ECD.
(1)求证:AB·DE=CD·BE;
(2)连接BD、AC,若AB∥CD,则结论“四边形ABDC一定是梯形”是否正确,若正确请证明;若不正确,请举出反例.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com