
分析 设方程2mx2-x-m=0的两个根为x1,x2,由根与系数的关系可得出x1•x2=-$\frac{1}{2}$,再由x1=1即可得出结论.
解答 解:设方程2mx2-x-m=0的两个根为x1,x2,
∴x1•x2=$\frac{c}{a}$=$\frac{-m}{2m}$=-$\frac{1}{2}$,
∵x1=1,
∴x2=-$\frac{1}{2}$.
故答案为:-$\frac{1}{2}$.
点评 本题考查了根与系数的关系,解题的关键是根据方程解析式结合根与系数的关系得出x1•x2=-$\frac{1}{2}$.本题属于基础题,难度不大,解决该题型题目时,根据根与系数的关系找出两根之和与两根之积是关键.


科目:初中数学 来源: 题型:解答题
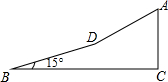 如图,某校八年级(1)班学生利用寒假期间到郊区进行社会实践活动,活动之余,同学们准备攀登附近的一个小山坡,从B点出发,沿坡脚15°的坡面以5千米/时的速度行至D点,用了10分钟,然后沿坡比为1:$\sqrt{3}$的坡面以3千米/时的速度达到山顶A点,用了5分钟,求小山坡的高(即AC的长度)(精确到0.01千米)(sin15°≈0.2588,cos15°≈0.9659,$\sqrt{3}$≈1.732)
如图,某校八年级(1)班学生利用寒假期间到郊区进行社会实践活动,活动之余,同学们准备攀登附近的一个小山坡,从B点出发,沿坡脚15°的坡面以5千米/时的速度行至D点,用了10分钟,然后沿坡比为1:$\sqrt{3}$的坡面以3千米/时的速度达到山顶A点,用了5分钟,求小山坡的高(即AC的长度)(精确到0.01千米)(sin15°≈0.2588,cos15°≈0.9659,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
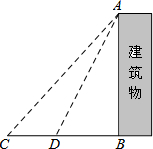 某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某艺术类学校进行绘画特长生的招生工作,每名考生需要参加“素描”“色彩”“速写”三个项目的测试,三个项目的满分均为100分,“素描”“色彩”“速写”按照4:4:2的比例计算得到选手最终成就,现有20名考生报名参加测试,测试结束后,考生的素描成绩如下(单位:分):
某艺术类学校进行绘画特长生的招生工作,每名考生需要参加“素描”“色彩”“速写”三个项目的测试,三个项目的满分均为100分,“素描”“色彩”“速写”按照4:4:2的比例计算得到选手最终成就,现有20名考生报名参加测试,测试结束后,考生的素描成绩如下(单位:分):| 分组 | 人数(频数) |
| 60-70 | 1 |
| 70-80 | 2 |
| 80-90 | 9 |
| 90-100 | 8 |
| 合计 | 20 |
| 项目 成绩 | 素描 | 色彩 | 速写 |
| 甲 | 98 | 93 | 95 |
| 乙 | 95 | 95 | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com