
【题目】如图,△ABC中,∠B=60°,∠C=75°,AC=3 ![]() ,求AB的长.
,求AB的长.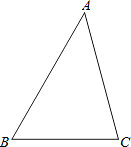
【答案】解:过点C作CD⊥AB于点D,
∵∠B=60°,∠C=75°,
∴∠A=45°,
在△ADC中,AC=3 ![]() ,
,
∵sinA= ![]() ,
,
∴AD=sin45°×3 ![]() =3=CD,
=3=CD,
在△BDC中,∠DCB=30°,
∵ctgB= ![]()
∴BD=cot60°×3= ![]() ,
,
∴AB= ![]() +3,
+3,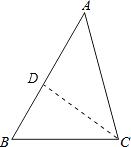
【解析】过点C作CD⊥AB于点D,先根据三角形内角和定理计算出∠A=45°,在Rt△ADC中,利用∠A的正弦可计算出CD,进而求得AD,然后在Rt△BDC中,利用∠B的余切可计算出BD,进而就可求得AB.
【考点精析】掌握三角形的内角和外角是解答本题的根本,需要知道三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )

A. 8 B. 16 C. 24 D. 32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(3x-2y)2-2x(3x-2y);
(2)(2a+1)(4a2-2a+1);
(3)先化简,再求值:
(-x-2y)(x-2y)-(2y-x)2+(2x3-4x2y)÷2x,其 中x=-3,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC=2,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E,AD的垂直平分线交AB于点E,则△DEF的面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=-2x+100.(利润=售价-制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得350万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察图形:
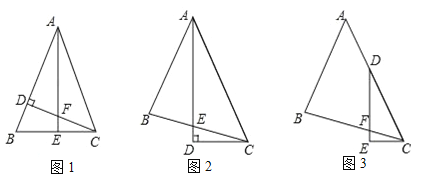
如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形_________________;
②线段AF与线段CE的数量关系是_________________;
(2)问题探究:
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
(3)拓展延伸:
如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC=![]() ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.
求证:DF=2CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的三边长分别为a,b,c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③a2=(b+c)(b-c);④a:b:c=5:12:13,其中能判断△ABC是直角三角形的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com