
����Ŀ����ͼ1,��ƽ��ֱ������ϵ��,ֱ��![]() ��������
��������![]() ����
����![]() ���㣬����
���㣬����![]() ,
,![]() .����������
.����������![]() �ύ�ڵ�
�ύ�ڵ�![]() ,��
,��![]() �ύ����һ��
�ύ����һ��![]() .
.

(1)��![]() ��ֵ���������ߵĽ���ʽ;
��ֵ���������ߵĽ���ʽ;
(2)��ͼ2.����![]() Ϊ�߶�
Ϊ�߶�![]() �ϵ�һ����(����
�ϵ�һ����(����![]() �غ�).�ֱ���
�غ�).�ֱ���![]() ��
��![]() Ϊб��,��ֱ��
Ϊб��,��ֱ��![]() ��ͬ��������ֱ����
��ͬ��������ֱ����![]() �͵���ֱ����
�͵���ֱ����![]() ,����
,����![]() ,��ȷ����
,��ȷ����![]() ������ʱ
������ʱ![]() �������.
�������.
(3)��ͼ3.����![]() ��
��![]() ,���߶�
,���߶�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ,ʹ����
,ʹ����![]() Ϊ���������������
Ϊ���������������![]() ����,������,��ֱ��д����
����,������,��ֱ��д����![]() ������;��������,��˵������.
������;��������,��˵������.
���𰸡���1��![]() ����2����
����2����![]() ����
����![]() ʱ��
ʱ��![]() ���ʱ
���ʱ![]() ,����
,����![]() ����3�����ڵ�
����3�����ڵ�![]() ����Ϊ
����Ϊ![]() ��
��![]() .
.
����������1����A��B�������һ�κ�������ʽ���m��n��ֵ��ȷ����A��B������������κ�������ʽ���b��c��ֵ������
��2���ɵ���ֱ�ǡ�APM�͵���ֱ�ǡ�DPN���õ���MPNΪֱ��������ֱ�DZ߳˻���һ���ʾ��������MPN��������ö��κ�������ȷ����������������ʱP�����꼴����
��3��������������������������Ƶñ��������AQ�ij������������ľ��빫ʽ���Q���꼴�ɣ�
��1����A��m��0����B��4��n������y=x��1����m=1��n=3����A��1��0����B��4��3����
��y=��x2+bx+c������A���B����![]() �������
�������![]() ������κ�������ʽΪy=��x2+6x��5��
������κ�������ʽΪy=��x2+6x��5��
��2����ͼ2����APM���DPN��Ϊ����ֱ�������������APM=��DPN=45�㣬���MPN=90�㣬���MPNΪֱ�����������x2+6x��5=0���õ�x=1��x=5����D��5��0������DP=5��1=4����AP=m������DP=4��m����PM=![]() m��PN=
m��PN=![]() ��4��m������S��MPN=
��4��m������S��MPN=![]() PMPN=
PMPN=![]() ��
��![]() m��
m��![]() ��4��m��=��
��4��m��=��![]() m2��m=��
m2��m=��![]() ��m��2��2+1���൱m=2����AP=2ʱ��S��MPN�������ʱOP=3����P��3��0����
��m��2��2+1���൱m=2����AP=2ʱ��S��MPN�������ʱOP=3����P��3��0����
��3����������ֱ��CD����ʽΪy=x��5����Q��x��x��5���������������BAD=��ADC=45�㣬���������������
������ABD�ס�DAQʱ��![]() =
=![]() ����
����![]() =
=![]() �������AQ=
�������AQ=![]() ���������ľ��빫ʽ������x��1��2+��x��5��2=
���������ľ��빫ʽ������x��1��2+��x��5��2=![]() �������x=
�������x=![]() ����ʱQ��
����ʱQ��![]() ����
����![]() ����
����
�ڵ���ABD�ס�DQAʱ��![]() =1����AQ=
=1����AQ=![]() ������x��1��2+��x��5��2=10�������x=2����ʱQ��2����3����
������x��1��2+��x��5��2=10�������x=2����ʱQ��2����3����
��������Q��������2����3����![]() ����
����![]() ����
����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�O�У���C��ֱ��AB�ӳ�����һ�㣬����C����O�����ߣ��е�ΪD������BD��
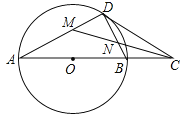
��1����֤����A=��BDC��
��2����CMƽ�֡�ACD���ҷֱ�AD��BD�ڵ�M��N����DM=1ʱ����MN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
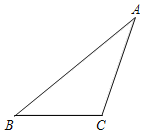
����Ŀ����ͼ10����������ABC�У���ACB��90�㣮
��1��������Ҫ����Ӧ��ͼ�Σ�
���ӳ�BC����D��ʹBD��2BC������AD��
������A��ֱ��BC�Ĵ��ߣ�����Ϊ��E��
������C��CG��AB��CG��AE���ڵ�F����AD���ڵ�G��
��2���ڣ�1����������ͼ���У���Ҫ������������⣮
����A��D֮��ľ������߶�_____�ij�����A���߶�BC���ڵ�ֱ�ߵľ������߶�___�ij���Լ����____mm����ȷ��1mm����
����˵����ACD����B+��BAC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽�ѧ���İ�ȫ��ʶ�������ȫУ��Χ�������ȡ����ѧ�������ʾ����飬���ݵ���������ѧ���İ�ȫ��ʶ�ֳɡ���������һ�㡱����ǿ������ǿ���ĸ���Σ������Ƴ����������в�������ͳ��ͼ��
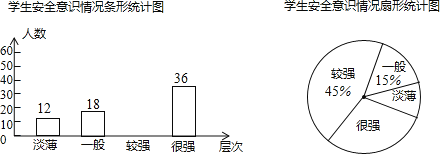
����������Ϣ������������⣺
��1���뽫����ͳ��ͼ����������
��2��������ǿ���͡���ǿ������Ϊ��ȫ��ʶ�ϸ�����ݳ�������Ľ���������У2000��ѧ���а�ȫ��ʶ�ϸ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ƽ���ı���ABCD������ֱ�ΪA����1��0����B��0��2����C��4��2����D��3��0������P��AD���ϵ�һ�����㣬����A����BP�ĶԳƵ�ΪA'����A'C����СֵΪ��������
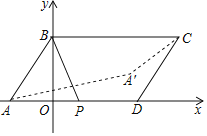
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���ı��ε�һ���Խ��߰��ı��ηֳ��������������Σ����ǰ������Խ��߽�����ı��εĺ�г�ߣ�����ı��ν�����г�ı��Σ������ξ��Ǻ�г�ı��Σ�

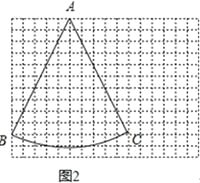
��1����ͼ1��������ABCD�У�AD��BC����BAD=120������C=75����BDƽ����ABC����֤��BD������ABCD�ĺ�г�ߣ�
��2����ͼ2����12��16������ͼ�ϣ�ÿ��С�����εı߳�Ϊ1����һ������BAC����A��B��C���ڸ���ϣ����ڴ������������������ͼ�ϸ���һ����D��ʹ����A��B��C��DΪ������ı��ε������Խ��߶��Ǻ�г�ߣ���������Ӧ�ĺ�г�ı��Σ�
��3���ı���ABCD�У�AB=AD=BC����BAD=90����AC���ı���ABCD�ĺ�г�ߣ�����BCD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��AB����O��һ���ң�OD��AB������ΪC������O�ڵ�D����E����O�ϣ�
��1������AOD=52��������DEB�Ķ�����
��2����OC=3��OA=5����AB�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
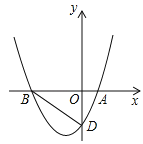
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=![]() x2+bx+c��ͼ����x�ύ�ڵ�A��2��0����B����4��0������y�ύ�ڵ�D��
x2+bx+c��ͼ����x�ύ�ڵ�A��2��0����B����4��0������y�ύ�ڵ�D��
��1���������ߵĽ���ʽ��
��2������BD����P�������ߵĶԳ����ϣ���QΪƽ����һ�㣬�ı���PBQD�ܷ��Ϊ���Σ����ܣ��������P�����ꣻ�����ܣ���˵�����ɣ�
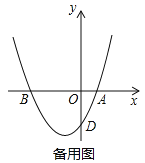
��3��������������һ��M������M��A��ֱ��MA��y���ڵ�C������BC������MBO=��BCO����ֱ��д����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�ƻ��ӱ�����ס����������ͺ���Ʒ��30�ֽ�������.������ס������ض�����·��·��������ͼ��ʾ������·�ĵ�λ�˼�Ϊ2Ԫ/����ǧ�ף�����·�ĵ�λ�˼�Ϊ3Ԫ/����ǧ�ף�.
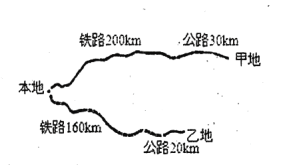
��1����˾�ƻ��ӱ���������亣��Ʒ![]() �֣����ܷ���
�֣����ܷ���![]() ��Ԫ����
��Ԫ����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2����˾Ҫ���˵��صĺ���Ʒ�����������ڵõ��ҵصĺ���Ʒ������2������![]() Ϊ����ʱ�����˷�
Ϊ����ʱ�����˷�![]() ��ͣ�������˷��Ƕ���Ԫ��(�ο���ʽ�������˷�
��ͣ�������˷��Ƕ���Ԫ��(�ο���ʽ�������˷�![]() ��λ�˼�
��λ�˼�![]() �������
�������![]() ����������
����������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com