
����Ŀ��ij���г����ƻ�һ���������г�1400����ƽ��ÿ������200��������������ԭ��ʵ��ÿ����������ƻ�������г��룮�±���ij�ܵ����������������Ϊ����������Ϊ������
���� | һ | �� | �� | �� | �� | �� | �� |
���� | +5 | -2 | -5 | +9 | -10 | +16 | -9 |
��1�����ݼ�¼�����ݿ�֪�ó��������������г���������
��2����������һ��Ȳ������ٵ�һ����������г���������
��2�����ݼ�¼�����ݿ�֪�ó�����ʵ���������г���������
��4���ó�ʵ��ÿ�ܼƼ������ƣ�ÿ����һ�����ɵ�100Ԫ���������������������ÿ������30Ԫ��������һ����40Ԫ����ô�ó�������һ�ܵĹ����ܶ��Ƕ���Ԫ��
���𰸡���1��209��2��26��3��1404��4��140260.
��������
��1�����ݳ�����Ϊ����������Ϊ�����û���200����������������.
��2������������Ϊ�������ģ���������С��Ϊ�������ٵģ��ֱ������������.
��3������������ӵõ�һ���ܵ����������ټ���һ��ƽ������1400������.
��4������ÿ��������200���Ļ����ϼ���������ͼ����Ĺ��ʣ������.
��1��������Ϊ����������Ϊ���������������������г�200+9=209������.
��2������ͼʾ��������һ����216�����������ٵ�һ����190�����ʲ�������һ��Ȳ������ٵ�һ����������г�216-190=26������.
��3����������![]() ��
��![]() ���������ʸó�����ʵ���������г�1404��.
���������ʸó�����ʵ���������г�1404��.
��4���������![]() Ԫ
Ԫ
���Ըù���������һ�ܵĹ����ܶ���140260Ԫ.
�ʴ�Ϊ����1��209��2��26��3��1404��4��140260.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��ƽ��ֱ������ϵ![]() ��,λ�ڵڶ����ĵ�
��,λ�ڵڶ����ĵ�![]() �ڷ���������
�ڷ���������![]() ��ͼ���ϣ���
��ͼ���ϣ���![]() ���
���![]() ����ԭ��
����ԭ��![]() �Գƣ�ֱ��
�Գƣ�ֱ��![]() ������
������![]() �����뷴��������
�����뷴��������![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() .
.

��1������![]() �������-2����
�������-2����![]() ������
������![]() ʱ���ֱ����
ʱ���ֱ����![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2������![]() �ĺ������ǵ�
�ĺ������ǵ�![]() �ĺ������4������
������4������![]() �������16����
�������16����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η��̣�x��3����x��2��=|m|��
��1����֤����������ʵ��m������������������ȵ�ʵ������
��2�������̵�һ������1����m��ֵ�����̵���һ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��
��![]() �����������ϣ���
�����������ϣ���![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() ����
����![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() ����
����![]() Ϊ�߶�
Ϊ�߶�![]() ���е�.����
���е�.����![]() �������ϣ��ҵ�
�������ϣ��ҵ�![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() .
.

��1�����![]() ��ʾ������
��ʾ������
��2����![]() �ӵ�
�ӵ�![]() ���������յ�
���������յ�![]() �˶�.��
�˶�.��![]() �е�Ϊ
�е�Ϊ![]() .���ú�
.���ú�![]() ����ʽ��ʾ�߶�
����ʽ��ʾ�߶�![]() �ij�.
�ij�.
��3���ڣ�2���������£���![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������������ѭ��С����Ϊ���������ϣ��������Ӧ���⣺
����֪������![]() дΪС����ʽ��Ϊ
дΪС����ʽ��Ϊ![]() ����֮������ѭ��С��
����֮������ѭ��С��![]() д�ɷ�����ʽ��
д�ɷ�����ʽ��![]() ��һ��أ��κ�һ������ѭ��С��������д�ɷ�����ʽ��������ԣ�Ӧ����д�أ�
��һ��أ��κ�һ������ѭ��С��������д�ɷ�����ʽ��������ԣ�Ӧ����д�أ�
�����֣���������ѭ��С��![]() Ϊ���������ۣ�
Ϊ���������ۣ�
��![]() ��x����
��x����![]() ��0.777����֪��10x��7.777������10x��x��7���ⷽ�̣���x��
��0.777����֪��10x��7.777������10x��x��7���ⷽ�̣���x��![]() ������
������![]() ��
��![]() ��
��
�����̽������������ѭ��С��![]() Ϊ��������һ�������ۣ�
Ϊ��������һ�������ۣ�
����ѭ��С��![]() ��0.737373��������ѭ��������λ�������������ۿ����뵽����������
��0.737373��������ѭ��������λ�������������ۿ����뵽����������
��![]() ��x����
��x����![]() ��0.737373����֪��100x��73.7373��������100x��x��73���ⷽ�̣���x��
��0.737373����֪��100x��73.7373��������100x��x��73���ⷽ�̣���x��![]() �����ǵ�
�����ǵ�![]() ��
��![]()
��������⣩
��1�����������С��![]() д�ɷ�����ʽ����
д�ɷ�����ʽ����![]() ���� ����
���� ����
��2�����������С��![]() д�ɷ�����ʽ����
д�ɷ�����ʽ����![]() ���� ����
���� ����
��3���������Ϲ��̱Ƚ�![]() ��1�Ĵ�С��ϵ����˵��������ɣ�
��1�Ĵ�С��ϵ����˵��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ӳ˷�����Ϊ��������˵�һ�ּ��㷽��������15�������������ѧ��������������������ġ��㷨ͳ�ڡ�һ���б���Ϊ���̵ؽ���.��ͼ1������![]() ��������47�������У�����51�������У�Ȼ���Գ���47��ÿλ���ֳ��Գ���51��ÿλ���֣������������Ӧ�ĸ����У����б�м���������2397.
��������47�������У�����51�������У�Ȼ���Գ���47��ÿλ���ֳ��Գ���51��ÿλ���֣������������Ӧ�ĸ����У����б�м���������2397.

��1����ͼ2���������ӳ˷�����ʾ![]() ����
����![]() ��ֵΪ__________.
��ֵΪ__________.
��2����ͼ3���������ӳ˷�����ʾ������λ����ˣ���![]() ��ֵΪ___________.
��ֵΪ___________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����ǰ尴��ͼ���ã������н����У���ȷ���У� ���١�1=��3���������2=30������AC��DE���������2=30��������BC��AD���������2=30�������С�4=��C

A.�٢ڢ�B.�٢ڢ�C.�ۢ�D.�٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�����ԭ��O���������ż�ͷ����ÿ���ƶ�1����λ���ȣ����εõ���A1(0��1)��A2(1��1)��A3(1��0)��A4(2��0)��A5(2��1)���������A2018��������_____��
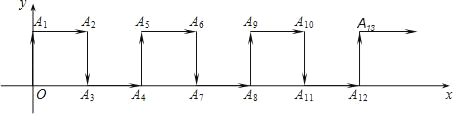
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�E��AD���е㣬�ӳ�CE��BA���ڵ�F������AC��DF��
��1����֤���ı���ACDF��ƽ���ı��Σ�
��2����CFƽ�֡�BCDʱ��д��BC��CD��������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com