练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

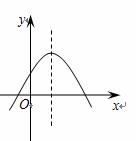
    如图，二次函数y=ax2+bx+c的图象开口向上，图象经过点（-1，2）和（1，0），且与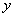轴相交于负半轴．给出四个结论：

    ① abc<0；   ②a+c=1；   ③ 2a+b>0；  

    其中结论正确的个数为（    ）(2014宁波一模改编)

    A．4            B．3                C．2                D．1


    C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


     设0＜k＜2，关于x的一次函数，当1≤x≤2时的最大值是（    ）

    （A）       （B）    （C）k       （D）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    从五个点（-2, 4）、（4, 2）、（2,3）、（2, -4）、（1,-8）中任取一点，在直线上的概率是（     ）

    A.          B.           C.          D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     已知甲、乙两种矿石中均含有金属A，其含量及每吨原料的购买单价如下表所示：

    金属A含量

    单价（万元/吨）

    甲矿石

    5%

    2.5

    乙矿石

    8%

    6

    已知用甲矿石提取每千克金属A要排放废气1吨，用乙矿石提取每千克金属A要排放废气0.5吨，若某厂要提取金属A20千克，并要求废气排放不超过16吨，问：该厂购买这两种原料的费用最少是多少万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    据市统计局年报，去年我市人均生产总值为104000元，104000用科学计数法表示为(  )  

    （A）1.0400×106元                 （B）0.10400×106元

    （C）1.04000×105元                 （D）10.400×104元

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    关于x的方程a(x＋m)2＋b＝0的解是x1＝－3，x2＝5（a，m，b均为常数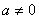，），则方程a(x＋m＋2)2＋b＝0的解是____________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


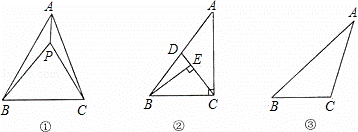
    如图①，P为△ABC内一点，连接PA、PB、PC，在△PAB、△PBC和△PAC中，如果存在一个三角形与△ABC相似，那么就称P为△ABC的自相似点．

    （1）如图②，已知Rt△ABC中，∠ACB=90°，∠ABC＞∠A，CD是AB上的中线，过点B作BE丄CD，垂足为E．试说明E是△ABC的自相似点；（4分）

    （2）在△ABC中，∠A＜∠B＜∠C．

    ①如图③，利用尺规作出△ABC的自相似点P（不写出作法，留作图痕迹）；（3分）

    ②若△ABC的内心P是该三角形的自相似点，求该三角形三个内角的度数．（3分）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在Rt△ABC中，∠ACB=90°，点D，E分别是边AB，AC的中点，延长BC到点F，使CF=BC .若AB=10，则EF的长是           .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


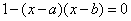     “如果二次函数y＝ax2＋bx＋c的图象与x轴有两个公共点，那么一元二次方程ax2＋bx＋c=0有两个不相等的实数根.”请根据你对这句话的理解，解决下面问题：若m、n（m<n）是关于x的方程的两根，且a < b， 则a、b、m、n 的大小关系是 

     A. m < a < b< n       B. a < m < n < b      C. a < m < b< n        D. m < a < n < b

    查看答案和解析>>

    同步练习册答案