
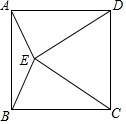
 如图,在正方形ABCD的内部作等边△CDE,连接AE,则∠DAE的度数为( )
如图,在正方形ABCD的内部作等边△CDE,连接AE,则∠DAE的度数为( )| A. | 80° | B. | 75° | C. | 70° | D. | 60° |
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x}{300}$=$\frac{2x+1.5}{300}$-93 | B. | $\frac{x}{300}$=$\frac{2x+1.5}{300}$+93 | ||
| C. | $\frac{x}{300}$=$\frac{2x+1.5}{300}$-$\frac{93}{3600}$ | D. | $\frac{x}{300}$=$\frac{2x+1.5}{300}$+$\frac{93}{3600}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查武汉市场某酸奶的质量情况 | |
| B. | 了解武汉市中小学生的视力情况 | |
| C. | 调查乘坐飞机的旅客是否携带了违禁物品 | |
| D. | 了解武汉市中学生课外阅读的情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
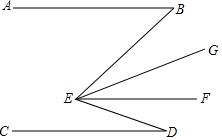 已知:如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,则∠GEF的度数为( )
已知:如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,则∠GEF的度数为( )| A. | 50° | B. | 40° | C. | 30° | D. | 20° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com