
 交AC于点E,F是
交AC于点E,F是 上的点,且
上的点,且 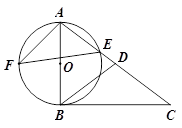
 的切线;
的切线; 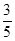 ,AE=
,AE=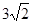 ,求sin∠AFE的值和AF的长.
,求sin∠AFE的值和AF的长.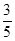 ,5
,5 .
. 的直径,
的直径, 的切线.………………………………………………………3分
的切线.………………………………………………………3分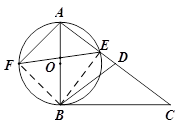
 的直径,
的直径,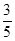 . …………………………………………………………………6分
. …………………………………………………………………6分 .
. 在Rt△ABE中,
在Rt△ABE中,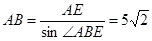 . ……………………………………8分
. ……………………………………8分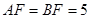 . …………………………………………………………………9分
. …………………………………………………………………9分

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源:不详 题型:单选题
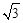 ,堤坝高BC=50m,则应水坡面AB的长度是【 】
,堤坝高BC=50m,则应水坡面AB的长度是【 】
| A.100m | B.100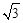 m m | C.150m | D.50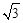 m m |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
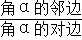 =
=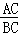 ,根据上述角的余切定义,解下列问题:
,根据上述角的余切定义,解下列问题: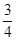 ,其中∠A为锐角,试求ctanA的值.
,其中∠A为锐角,试求ctanA的值.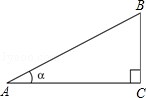
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
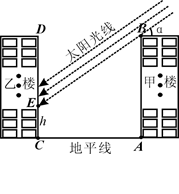
 ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
 ≈1.732).
≈1.732).查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
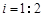 且O,A,B在同一条直线上.求电视塔OC的高度以及此人所在位置P的铅直高度PB.(测倾器高度忽略不计,结果保留根号形式)
且O,A,B在同一条直线上.求电视塔OC的高度以及此人所在位置P的铅直高度PB.(测倾器高度忽略不计,结果保留根号形式)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 取1.73).
取1.73).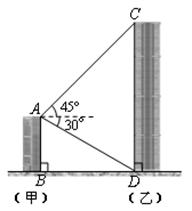
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com