
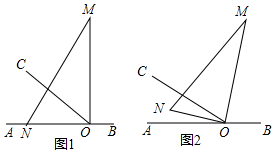
分析 (1)用角的度数除以转动速度即可得;
(2)根据∠AOC=30°、OM恰好平分∠BOC知∠BOM=75°,进而可知旋转的度数,结合旋转速度可得时间t;
(3)分别根据转动速度关系和OC平分∠MOB画图即可.
解答 解:(1)∵30÷3=10,
∴10秒后ON与OC重合;
(2)∵∠AON+∠BOM=90°,∠COM=∠MOB,
∵∠AOC=30°,
∴∠BOC=2∠COM=150°,
∴∠COM=75°,
∴∠CON=15°,
∴∠AON=∠AOC-∠CON=30°-15°=15°,
解得:t=15°÷3°=5秒;
(3)∵∠AON+∠BOM=90°,∠BOC=∠COM,
∵三角板绕点O以每秒3°的速度,射线OC也绕O点以每秒6°的速度旋转,
设∠AON为3t,∠AOC为30°+6t,
∴∠COM为$\frac{1}{2}$(90°-3t),
∵∠BOM+∠AON=90°,
可得:180°-(30°+6t)=$\frac{1}{2}$(90°-3t),
解得:t=$\frac{70}{3}$秒;
如图: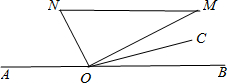
点评 此题考查了角的计算,关键是应该认真审题并仔细观察图形,找到各个量之间的关系求出角的度数是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 0 | D. | 不确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
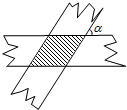 如图,把两条宽度都是1的纸条,其中一条对折后再两条交错地叠在一起,相交成角α,则重叠部分的面积是( )
如图,把两条宽度都是1的纸条,其中一条对折后再两条交错地叠在一起,相交成角α,则重叠部分的面积是( )| A. | 2sinα | B. | 2cosα | C. | $\frac{1}{sinα}$ | D. | $\frac{1}{2cosα}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-b=0 | B. | ab=1 | C. | a+b=0 | D. | ab=-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com