
分析 先算括号里面的,再算除法,最后选取合适的x的值代入进行计算即可.
解答 解:原式=[$\frac{x(x+2)}{{x}^{2}(x-2)}$-$\frac{x-1}{(x-2)^{2}}$]•$\frac{{x}^{2}(x-2)}{x-4}$
=$\frac{{x}^{2}-4-{x}^{2}+x}{x(x-2)^{2}}$•$\frac{{x}^{2}(x-2)}{x-4}$
=$\frac{x-4}{x(x-2)^{2}}$•$\frac{{x}^{2}(x-2)}{x-4}$
=$\frac{x}{x-2}$.
当x=3时,原式=3.
点评 本题考查的是分式的化简求值,分式求值题中比较多的题型主要有三种:转化已知条件后整体代入求值;转化所求问题后将条件整体代入求值;既要转化条件,也要转化问题,然后再代入求值.


科目:初中数学 来源: 题型:选择题
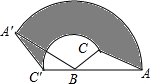 如图,在△ABC中,AB=12cm,BC=6cm,∠ABC=30°,把△ABC以点B为中心按逆时针方向旋转,使点C旋转到AB边的延长线上的C′处,那么AC边扫过的图形(图中阴影部分)的面积是( )cm2.(结果保留π)
如图,在△ABC中,AB=12cm,BC=6cm,∠ABC=30°,把△ABC以点B为中心按逆时针方向旋转,使点C旋转到AB边的延长线上的C′处,那么AC边扫过的图形(图中阴影部分)的面积是( )cm2.(结果保留π)| A. | 15π | B. | 60π | C. | 45π | D. | 75π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
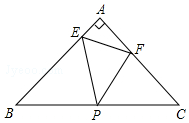 如图,在△ABC中,AB=AC=2,∠A=90°,P为BC的中点,E、F分别是AB、AC上的动点,∠EPF=45°.
如图,在△ABC中,AB=AC=2,∠A=90°,P为BC的中点,E、F分别是AB、AC上的动点,∠EPF=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
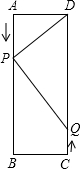 如图,矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB向点B移动(不与点A、B重合),一直到达点B为止;同时,点Q从点C出发沿CD向点D移动(不与点C、D重合).运动时间设为t秒.
如图,矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB向点B移动(不与点A、B重合),一直到达点B为止;同时,点Q从点C出发沿CD向点D移动(不与点C、D重合).运动时间设为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com