
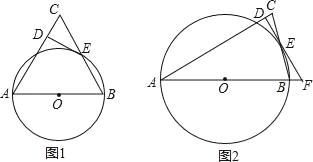
【题目】如图1,在△ABC中,AB=AC,以△ABC的边AB为直径的⊙O角边BC于点E,过点E作DE⊥AC交AC于D.
(1)求证:DE是⊙O的切线;
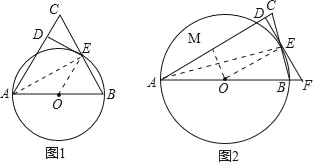
(2)如图2,若线段AB、DE的延长线交于点F,∠C=75°,CD=2﹣![]() ,求⊙O的半径和EF的长.
,求⊙O的半径和EF的长.
【答案】(1)证明见解析;(2)半径为2,EF=![]() .
.
【解析】分析:(1)连接OE,AE,利用圆周角定理的“三线合一”证明;(2)过点O作OM⊥AC,设OM=x,用含x的式子表示出AM,DM,AC的长,由AC-AM-MD=2﹣![]() ,列方程求x,得到圆的关系,再在Rt△OEF中求EF.
,列方程求x,得到圆的关系,再在Rt△OEF中求EF.
详解:(1)如图1,连接OE,AE,
∵AB是⊙O的直径,∴∠EBA=90°,
∴AE⊥BC,AB=AC,∴BE=CE,
∵AO=OB,∴OE∥AC,
∵DE⊥AC,∴DE⊥OE,
∴DE是⊙O的切线;
(2)如图2,过点O作OM⊥AC,
∵∠C=75°,AB=AC,∴∠B=∠C=75°,∴∠A=180°﹣75°﹣75°=30°,
设OM=x,则OA=OB=OE=2x,AM=![]() x,OD⊥DE,DE⊥AC,
x,OD⊥DE,DE⊥AC,
∴四边形OEDM是矩形,∴DM=OE=2x,
OE=![]() AC,可得:4x=
AC,可得:4x=![]() x+2x+2﹣
x+2x+2﹣![]() ,x=1,
,x=1,
∴OE=OB=2,即半径为2,
在直角△OEF中,∠EOF=∠A=30°,
∴![]() =tan30°=
=tan30°=![]() ,
,
EF=![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
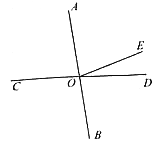
【题目】如图,AB、CD交于点O,∠AOE=4∠DOE,∠AOE的余角比∠DOE小10°(题中所说的角均是小于平角的角).
(1)求∠AOE的度数;
(2)请写出∠AOC在图中的所有补角;
(3)从点O向直线AB的右侧引出一条射线OP,当∠COP=∠AOE+∠DOP时,求∠BOP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
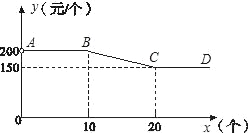
【题目】永定土楼是世界文化遗产“福建土楼”的组成部分,是闽西的旅游胜地.“永定土楼”模型深受游客喜爱.图中折线(AB∥CD∥x轴)反映了某种规格土楼模型的单价y(元)与购买数量x(个)之间的函数关系.
(1)求当10≤x≤20时,y与x的函数关系式;
(2)已知某旅游团购买该种规格的土楼模型总金额为2625元,问该旅游团共购买这种土楼模型多少个?(总金额=数量×单价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:F(n)=![]() ,例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)=
,例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)=![]() .
.
(1)如果一个正整数a是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1.
(2)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
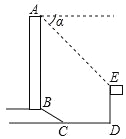
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆低端D到大楼前梯砍底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:![]() ,则大楼AB的高度为_________米.
,则大楼AB的高度为_________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
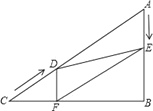
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出t的值,如果不能,说明理由;
(3)在运动过程中,四边形BEDF能否为正方形?若能,求出t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形中满足条件的是( )
①平行四边形;②菱形;③矩形;④对角线互相垂直的四边形.
A. ①③B. ②③C. ③④D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售A型和B型两种型号的电脑,销售一台A型电脑可获利120元,销售一台B型电脑可获利140元.该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的3倍.设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y与x的关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售利润最大?
(3)若限定商店最多购进A型电脑60台,则这100台电脑的销售总利润能否为13600元?若能,请求出此时该商店购进A型电脑的台数;若不能,请求出这100台电脑销售总利润的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮步行上山游玩,设小亮出发x min加后行走的路程为y m.图中的折线表示小亮在整个行走过程中y与x的函数关系,
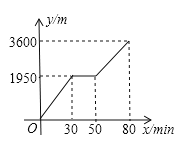
(1)小亮行走的总路程是____________m,他途中休息了____________min.
(2)当50![]() 80时,求y与x的函数关系式.
80时,求y与x的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com