
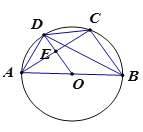
【题目】如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙D于点D,交AC于点E,连接AD,BD,CD若AB=10,cos∠ABC=![]() ,则tan∠DBC的值是( )
,则tan∠DBC的值是( )
A.![]() B.
B.![]() C.2D.
C.2D.![]()
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=(x﹣a﹣1)(x﹣a+1)﹣3a+7(其中x是自变量)的图象与x轴没有公共点,且当x<﹣1时,y随x的增大而减小,则实数a的取值范围是_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动.过点P作PE∥BC交AD于点E,连结EQ.设动点运动时间为x秒.
现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动.过点P作PE∥BC交AD于点E,连结EQ.设动点运动时间为x秒.
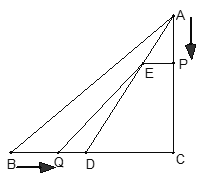
(1)用含x的代数式表示AE、DE的长度;
(2)当点Q在BD(不包括点B、D)上移动时,设![]() 的面积为
的面积为![]() ,求
,求![]() 与月份
与月份![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)当![]() 为何值时,
为何值时,![]() 为直角三角形.
为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文明小区50平方米和80平方米两种户型的住宅,50平方米住宅套数是80平方米住宅套数的2倍.物管公司月底按每平方米2元收取当月物管费,该小区全部住宅都人住且每户均按时全额缴纳物管费.
(1)该小区每月可收取物管费90 000元,问该小区共有多少套80平方米的住宅?
(2)为建设“资源节约型社会”,该小区物管公司5月初推出活动一:“垃圾分类送礼物”,50平方米和80平方米的住户分别有40%和20%参加了此次括动.为提离大家的积扱性,6月份准备把活动一升级为活动二:“拉圾分类抵扣物管费”,同时终止活动一.经调査与测算,参加活动一的住户会全部参加活动二,参加活动二的住户会大幅增加,这样,6月份参加活动的50平方米的总户数在5月份参加活动的同户型户数的基础上将增加![]() ,每户物管费将会减少
,每户物管费将会减少![]() ;6月份参加活动的80平方米的总户数在5月份参加活动的同户型户数的基础上将增加
;6月份参加活动的80平方米的总户数在5月份参加活动的同户型户数的基础上将增加![]() ,每户物管费将会减少
,每户物管费将会减少![]() .这样,参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少
.这样,参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某演唱会购买门票的方式有两种
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元;(注方式一中总费用=广告费用+门票费用)
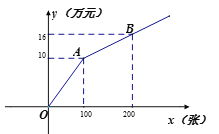
方式二:按如图所示的购买门票方式.
设购买门票x张,总费用为y万元.
(1)求按方式一购买时y与x的函数关系式
(2)若甲、乙两个单位分采用方式一,方式二购买本场演唱会门共400张,且乙单位购买超过100张,两单位共花费27.2万元,求甲、乙两单位各购买门票多少张?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月22日是第50个世界地球日,某校在八年级5个班中,每班各选拔10名学生参加“环保知识竞赛”并评出了一、二、三等奖各若干名,学校将获奖情况绘成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题:
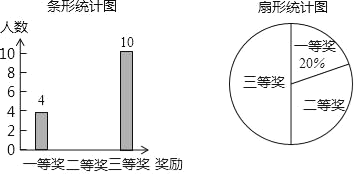
(1)求本次竞赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)如果该校八年级有800人,请你估计获奖的同学共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲地有42吨货物要运到乙地,有大、小两种货车可供选择,具体收费情况如表:
类型 | 载重量(吨) | 运费(元/车) |
大货车 | 8 | 450 |
小货车 | 5 | 300 |
运完这批货物最少要支付运费_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(-1,O)、C(3,0),点B为抛物线顶点,直线BD为抛物线的对称轴,点D在x轴上,连接AB、BC.

⑴如图1,若∠ABC=60°,则点B的坐标为______________;
⑵如图2,若∠ABC=90°,AB与y轴交于点E,连接CE.
①求这条抛物线的解析式;
②点P为第一象限抛物线上一个动点,设△PEC的面积为S,点P的横坐标为m,求S关于m的函数关系武,并求出S的最大值;
③如图3,连接OB,抛物线上是否存在点Q,使直线QC与直线BC所夹锐角等于∠OBD,若存在请直接写出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com