
分析 先化简题目中的式子,然后在0,1,2,3中选取一个使得原分式有意义的值代入化简后的式子即可解答本题.
解答 解:($\frac{{x}^{2}+4}{x}$-4)÷$\frac{{x}^{2}-4}{{x}^{2}-2x}$-$\frac{x-{x}^{2}}{x-1}$
=$\frac{{x}^{2}+4-4x}{x}×\frac{x(x-2)}{(x+2)(x-2)}-\frac{x(1-x)}{x-1}$
=$\frac{(x-2)^{2}}{x}×\frac{x}{x+2}+x$
=$\frac{{x}^{2}-4x+4}{x+2}+x$
=$\frac{{x}^{2}-4x+4+{x}^{2}+2x}{x+2}$
=$\frac{2{x}^{2}-2x+4}{x+2}$,
当x=3时,原式=$\frac{2×{3}^{2}-2×3+4}{3+2}=\frac{16}{5}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法,注意x不能等于0,1,2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
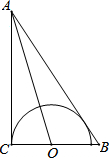 如图,在Rt△ABC中,∠ACB=90°,∠BAC的角平分线交BC于点O,OC=2,以点O为圆心OC为半径作圆.
如图,在Rt△ABC中,∠ACB=90°,∠BAC的角平分线交BC于点O,OC=2,以点O为圆心OC为半径作圆.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
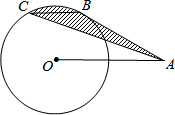 如图,A是半径为2的⊙O外的一点,OA=4,AB切⊙O于点B,弦BC∥OA,连接AC,则图中阴影部分的面积为$\frac{2}{3}$π.
如图,A是半径为2的⊙O外的一点,OA=4,AB切⊙O于点B,弦BC∥OA,连接AC,则图中阴影部分的面积为$\frac{2}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
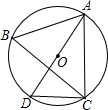 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5$\sqrt{3}$,
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5$\sqrt{3}$,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
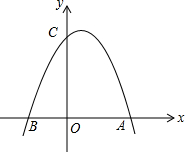 如图,已知抛物线经过点A(3,0)、B(-2,0)、C(0,6).
如图,已知抛物线经过点A(3,0)、B(-2,0)、C(0,6).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
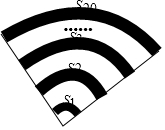 手机上常见的wifi标志如图所示,它由若干条圆心相同的圆弧组成,其圆心角为90°,最小的扇形半径为1,若每两个相邻圆弧的半径之差为1,由里往外的阴影部分的面积依次记为S1、S2、S3…,则S1+S2+S3+…+S20=205π.
手机上常见的wifi标志如图所示,它由若干条圆心相同的圆弧组成,其圆心角为90°,最小的扇形半径为1,若每两个相邻圆弧的半径之差为1,由里往外的阴影部分的面积依次记为S1、S2、S3…,则S1+S2+S3+…+S20=205π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com