
【题目】观察下列两个等式:![]() ,
,![]() ,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对
,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对![]() ,
,![]() ,都是“共生有理数对”.
,都是“共生有理数对”.
(1)数对![]() ,
,![]() 中是“共生有理数对”的是 ;
中是“共生有理数对”的是 ;
(2)若(m,n)是“共生有理数对”,则(﹣n,﹣m) “共生有理数对”(填“是”或“不是”);
(3)请再写出一对符合条件的“共生有理数对”为 ;(注意:不能与题目中已有的“共生有理数对”重复)
(4)若(a,3)是“共生有理数对”,求a的值.
【答案】(1)![]() ;(2)是;(3)
;(2)是;(3)![]() 或
或![]() 等;(4)a=-2
等;(4)a=-2
【解析】
(1)根据“共生有理数对”的定义即可判断;
(2)根据“共生有理数对”的定义即可解决问题;
(3)根据“共生有理数对”的定义即可判断;
(4)根据“共生有理数对”的定义,构建方程即可解决问题.
解:(1)-2-1=-3,-2×1+1=1,
∴-2-1≠-2×1+1,
∴(-2,1)不是“共生有理数对”,
∵3-![]() =
=![]() ,3×
,3×![]() +1=
+1=![]() ,
,
∴3-![]() =3×
=3×![]() +1,
+1,
∴(3,![]() )是“共生有理数对”;
)是“共生有理数对”;
(2)是.
理由:- n -(- m)=- n + m =m-n,
-n(-m)+1=mn+1,
∵(m,n)是“共生有理数对”,
∴m-n=mn+1,
∴-n+m=mn+1,
∴(-n,-m)是“共生有理数对”;
(3)![]() 或
或![]() 等;
等;
理由:∵![]() ,
,![]() ,
,
∴![]()
∴![]() 是“共生有理数对”,
是“共生有理数对”,
∵![]() ,
,![]() ,
,
∴![]()
∴![]() 是“共生有理数对”;
是“共生有理数对”;
(4)由题意得:
a-3=3a+1,
解得a=-2.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
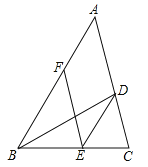
【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.
(1)求证:四边形ADEF是平行四边形;
(2)若∠ABC=60°,BD=4,求平行四边形ADEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,按照这种规律下去,第n次移动到点An,如果点An,与原点的距离不少于20,那么n的最小值是( )

A. 11B. 12C. 13D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
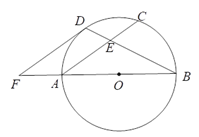
【题目】如图,AB是⊙O的直径,C是⊙O上一点,D是![]() 的中点,BD交AC于点E,过点D作DF∥AC交BA的延长线于点F.
的中点,BD交AC于点E,过点D作DF∥AC交BA的延长线于点F.
(1)求证:DF是⊙O的切线;
(2)若AF=2,FD=4,求tan∠BEC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
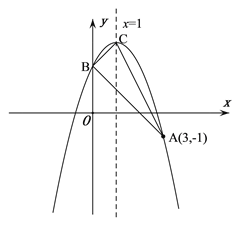
【题目】如图,抛物线![]() 的顶点为C,对称轴为直线
的顶点为C,对称轴为直线![]() ,且经过点A(3,-1),与y轴交于点B.
,且经过点A(3,-1),与y轴交于点B.
(1)求抛物线的解析式;
(2)判断△ABC的形状,并说明理由;
(3)经过点A的直线交抛物线于点P,交x轴于点Q,若![]() ,试求出点P的坐标.
,试求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边
表示直角三角形的两直角边![]() ,下列四个说法:①
,下列四个说法:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中说法正确的是
;其中说法正确的是![]()
![]()
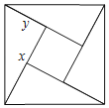
A. ①②B. ①②③C. ①②④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OC在∠BOD内.
(1)如果∠AOC和∠BOD都是直角.
①若∠BOC=60°,则∠AOD的度数是 ;
②猜想∠BOC与∠AOD的数量关系,并说明理由;
(2)如果∠AOC=∠BOD=x°,∠AOD=y°,求∠BOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
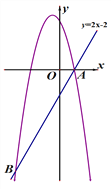
【题目】已知直线y=2x-2与抛物线![]() 交于点A(1,0)和点B,且m<n.
交于点A(1,0)和点B,且m<n.
(1)当m=![]() 时,直接写出该抛物线顶点的坐标.
时,直接写出该抛物线顶点的坐标.
(2)求点B的坐标(用含m的代数式表示).
(3)设抛物线顶点为C,记△ABC的面积为S.
①![]() ,求线段AB长度的取值范围;
,求线段AB长度的取值范围;
②当![]() 时,求对应的抛物线的函数表达式
时,求对应的抛物线的函数表达式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com