
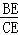 = .
= .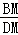 = ;
= ;
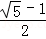
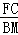 =
=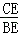 =
=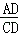 =
= ①,
①,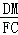 =
=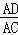 =
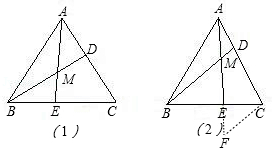
= ②,观察①②的乘积,可得BM、DM的数量关系.
②,观察①②的乘积,可得BM、DM的数量关系.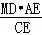 ,DC=
,DC=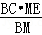 ,运用比例的性质合理变形,问题可求.
,运用比例的性质合理变形,问题可求.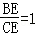 ;
; AM,(30°角所对的直角边等于斜边的一半)
AM,(30°角所对的直角边等于斜边的一半)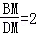 .
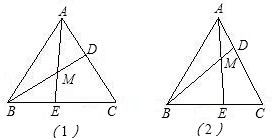
.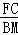 =
= =
=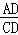 =
= ①,
①, =
= =
=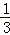 ②,
②,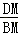 =
=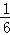 ,
,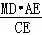 ③,DC=
③,DC=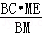 ④,
④,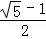 AD,
AD,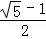 .
.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源:不详 题型:解答题
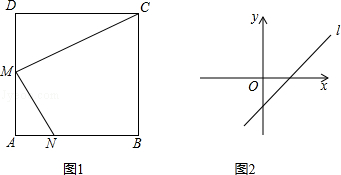
 ;
;查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.6条 | B.3条 | C.4条 | D.5条 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
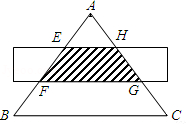
| A.4cm2 | B.2cm2 | C.3 cm2 cm2 | D.3cm2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com