
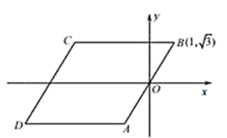
【题目】如图,已知四边形ABCD是菱形,BC∥x轴,点B的坐标是(1,![]() ),坐标原点O是AB的中点.动圆⊙P的半径是
),坐标原点O是AB的中点.动圆⊙P的半径是![]() ,圆心在x轴上移动,若⊙P在运动过程中只与菱形ABCD的一边相切,则点P的横坐标m 的取值范围是_________.
,圆心在x轴上移动,若⊙P在运动过程中只与菱形ABCD的一边相切,则点P的横坐标m 的取值范围是_________.
【答案】![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
若⊙P在运动过程中只与菱形ABCD的一边相切,则需要对此过程分四种情况讨论,根据已知条件计算出m的取值范围即可.
解:由B点坐标(1,![]() ),及原点O是AB的中点可知AB=2,直线AB与x轴的夹角为60°,
),及原点O是AB的中点可知AB=2,直线AB与x轴的夹角为60°,
又∵四边形ABCD是菱形,
∴AD=AB=BC=CD=2,
设DC与x轴相交于点H,则OH=4,
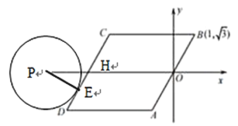
(1)当⊙P与DC边相切于点E时,连接PE,如图所示,
由题意可知PE=![]() ,PE⊥DC,∠PHE=60°,
,PE⊥DC,∠PHE=60°,
∴PH=2,
∴此时点P坐标为(-6,0),所以此时![]() .
.
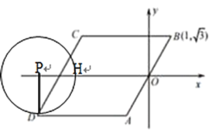
(2)当⊙P只与AD边相切时,如下图,
∵PD=![]() ,∴PH=1,
,∴PH=1,
∴此时![]() ,
,
当⊙P继续向右运动,同时与AD,BC相切时,PH=1,所以此时![]() ,
,
∴当![]() 时,⊙P只与AD相切;
时,⊙P只与AD相切;
 ,
,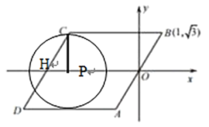
(3)当⊙P只与BC边相切时,如下图,
⊙P与AD相切于点A时,OP=1,此时m=-1,
⊙P与AD相切于点B时,OP=1,此时m=1,
∴当![]() ,⊙P只与BC边相切时;
,⊙P只与BC边相切时;
 ,
,
(4)当⊙P只与BC边相切时,如下图,
由题意可得OP=2,
∴此时![]() .
.
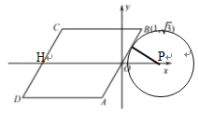
综上所述,点P的横坐标m 的取值范围![]() 或
或![]() 或
或![]() 或
或![]() .
.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】当今社会人们越来越离不开网络,电脑、手机被普遍使用,与此同时人们的视力也大大受到影响,2019年初某企业以25万元购得某项护目镜生产技术后,再投人100万元购买生产设备,进行该护目镜的生产加工,已知生产这种护目镜的成本价为每件20元,经过市场调研发现该产品的销售单价定在![]() 元比较合理,并且该产品的年销售量
元比较合理,并且该产品的年销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的函数关系式为
(元)之间的函数关系式为![]() .(年获利=年销售收入-生产成本-投资成本)
.(年获利=年销售收入-生产成本-投资成本)
(1)求该公司第一年的年获利![]() (万元)与销售单价
(万元)与销售单价![]() (元)之间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最小亏损是多少?
(元)之间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最小亏损是多少?
(2)2020年初我国爆发新冠肺炎,该公司决定向红十字会捐款20万元,另外每销售一件产品,就抽出1元钱作为捐款,若除去第一年的最大盈利(或最小亏损)以及第二年的捐款后,到2020年底,两年的总盈利不低于57.5万元,请你确定此时销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,当
,当![]() 时,
时,![]() 点坐标为
点坐标为![]() ;当
;当![]() 时,
时,![]() 点坐标为
点坐标为![]() ,则称点
,则称点![]() 为点
为点![]() 的
的![]() 分变换点(其中
分变换点(其中![]() 为常数).例如:
为常数).例如:![]() 的0分变换点坐标为
的0分变换点坐标为![]() .
.
(1)点![]() 的1分变换点坐标为 ;点
的1分变换点坐标为 ;点![]() 的1分变换点在反比例函数
的1分变换点在反比例函数![]() 图像上,则
图像上,则![]() ;若点
;若点![]() 的1分变换点直线
的1分变换点直线![]() 上,则
上,则![]() ;
;
(2)若点![]() 在二次函数
在二次函数![]() 的图像上,点
的图像上,点![]() 为点
为点![]() 的3分变换点.
的3分变换点.
①直写出点![]() 所在函数的解析式;
所在函数的解析式;
②求点![]() 所在函数的图像与直线
所在函数的图像与直线![]() 交点坐标;
交点坐标;
③当![]() 时,点
时,点![]() 所在函数的函数值
所在函数的函数值![]() ,直接写出
,直接写出![]() 的取值范围;
的取值范围;
(3)点![]() ,
,![]() ,若点
,若点![]() 在二次函数
在二次函数![]() 的图像上,点
的图像上,点![]() 为点
为点![]() 的
的![]() 分变换点.当点
分变换点.当点![]() 所在函数的图像与线段
所在函数的图像与线段![]() 有两个公共点时,直接写出
有两个公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
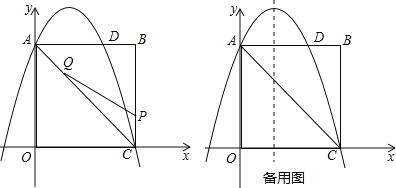
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在参加了成都市教育质量综合评价学业素养测试后,随机抽取八年级部分学生,针对发展水平四个维度:A﹣阅读素养、B﹣数学素养、C﹣科学素养、D﹣人文素养,开展了“你最需要提升的学业素养”问卷调查(每名学生必选且只能选择一项).现将调查的结果绘制成如图两幅不完整的统计图.
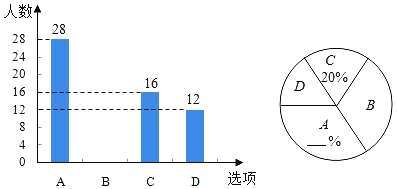
(1)求本次调查的学生总人数,并补全两幅统计图;
(2)求扇形统计图中的选项D对应的扇形圆心角的度数;
(3)该校八年级共有学生400人,请估计全年级选择选项B的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB为⊙O的直径,弦CD⊥AB于点E,在CD的延长线上取一点P,PG与⊙O相切于点G,连接AG交CD于点F.
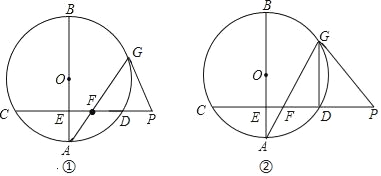
(Ⅰ)如图①,若∠A=20°,求∠GFP和∠AGP的大小;
(Ⅱ)如图②,若E为半径OA的中点,DG∥AB,且OA=2![]() ,求PF的长.
,求PF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com