
【题目】在国家政策的宏观调控下,某市的商品房成交价由今年9月份的14000元/m2下降到11月份的12600元/m2.
(1)问10、11两月平均每月降价的百分率是多少?(参考数据:![]() 0.95)
0.95)
(2)如果房价继续回落,按此降价的百分率,你预测到12月份该市的商品房成交均价是否会跌破12000元/m2?请说明理由.
【答案】(1)10、11两月平均每月降价的百分率是5%;(2)会跌破12000元/m2.理由见解析.
【解析】
(1)设10、11两月平均每月降价的百分率是x,那么10月份的房价为14000(1-x),11月份的房价为14000(1-x)2,然后根据11月份的12600元/m2即可列出方程解决问题;
(2)根据(1)的结果可以计算出11月份商品房成交均价,然后和12000元/m2进行比较即可作出判断.
(1)设10、11两月平均每月降价的百分率是x,
则10月份的成交价是14000﹣14000x=14000(1﹣x),
11月份的成交价是14000(1﹣x)﹣14000(1﹣x)x=14000(1﹣x)(1﹣x)=14000(1﹣x)2,
∴14000(1﹣x)2=12600,
∴(1﹣x)2=0.9,∴x1≈0.05=5%,x2≈1.95(不合题意,舍去).
答:10、11两月平均每月降价的百分率是5%;
(2)会跌破12000元/m2.
如果按此降价的百分率继续回落,估计12月份该市的商品房成交均价为:
12600(1﹣x)2=12600×0.952=11371.5<12000.
由此可知12月份该市的商品房成交均价会跌破12000元/m2.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以每秒1cm的速度移动,同时,点Q从点B出发沿BC边向点C以每秒2cm的速度移动,如果P、Q两点在分别到达B、C两点后就停止移动,回答下列问题:

(1)当运动开始后1秒时,求△DPQ的面积;
(2)当运动开始后![]() 秒时,试判断△DPQ的形状;
秒时,试判断△DPQ的形状;
(3)在运动过程中,存在这样的时刻,使△DPQ以PD为底的等腰三角形,求出运动时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明站在某广场一看台C处,从眼睛D处测得广场中心F的俯角为21°,若CD=1.6米,BC=1.5米,BC平行于地面FA,台阶AB的坡度为i=3:4,坡长AB=10米,则看台底端A点距离广场中心F点的距离约为(参考数据:sin21°≈0.36,cos21°≈0.93,tan21°≈0.38)( )
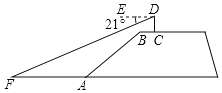
A.8.8米B.9.5米C.10.5米D.12米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于不在坐标轴上的任意一点P(x,y),我们把的P'(![]() ,
,![]() )称为点P的“倒影点”.直线y=﹣2x+1上有两点A、B,它们的倒影点A'、B'均在反比例函数y
)称为点P的“倒影点”.直线y=﹣2x+1上有两点A、B,它们的倒影点A'、B'均在反比例函数y![]() 的图象上,若AB
的图象上,若AB![]() ,则k的值为( )
,则k的值为( )
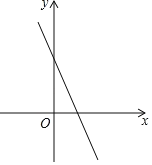
A.![]() B.
B.![]() C.5D.10
C.5D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图(2)所示,当P运动到BC中点时,△PAD的面积为( )
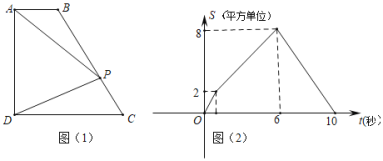
A. 4B. 5C. 6D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x、y轴的正半轴上,顶点B的坐标为(4,2)点M是边BC上的一个动点(不与B、C重合),反比例函数![]() (k>0,x>0)的图象经过点M且与边AB交于点N,连接MN.
(k>0,x>0)的图象经过点M且与边AB交于点N,连接MN.
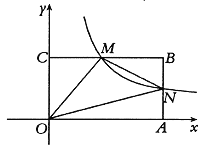
(1)当点M是边BC的中点时,求反比例函数的表达式;
(2)在点M的运动过程中,试证明:![]() 是一个定值.
是一个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形![]() 的边长为1,点
的边长为1,点![]() 是
是![]() 边上的一个动点(与
边上的一个动点(与![]() ,
,![]() 不重合),以
不重合),以![]() 为顶点在
为顶点在![]() 所在直线的上方作
所在直线的上方作![]()
(1)当![]() 经过点
经过点![]() 时,
时,
①请直接填空:![]() ________(可能,不可能)过
________(可能,不可能)过![]() 点:(图1仅供分析)
点:(图1仅供分析)
②如图2,在![]() 上截取
上截取![]() ,过
,过![]() 点作
点作![]() 垂直于直线
垂直于直线![]() ,垂足为点
,垂足为点![]() ,作
,作![]() 于
于![]() ,求证:四边形
,求证:四边形![]() 为正方形;
为正方形;
③如图2,将②中的已知与结论互换,即在![]() 上取点
上取点![]() (
(![]() 点在正方形
点在正方形![]() 外部),过
外部),过![]() 点作
点作![]() 垂直于直线
垂直于直线![]() ,垂足为点
,垂足为点![]() ,作
,作![]() 于
于![]() ,若四边形
,若四边形![]() 为正方形,那么
为正方形,那么![]() 与
与![]() 是否相等?请说明理由;
是否相等?请说明理由;
(2)当点![]() 在射线
在射线![]() 上且
上且![]() 不过点
不过点![]() 时,设
时,设![]() 交边
交边![]() 于
于![]() ,且
,且![]() .在
.在![]() 上存在点
上存在点![]() ,过
,过![]() 点作
点作![]() 垂直于直线
垂直于直线![]() ,垂足为点
,垂足为点![]() ,使得
,使得![]() ,连接
,连接![]() ,则当
,则当![]() 为何值时,四边形
为何值时,四边形![]() 的面积最大?最大面积为多少?
的面积最大?最大面积为多少?



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() (
(![]() )经过点
)经过点![]() 、B.
、B.
(1)求![]() 、
、![]() 满足的关系式及
满足的关系式及![]() 的值.
的值.
(2)当![]() 时,若
时,若![]() (
(![]() )的函数值随
)的函数值随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com