
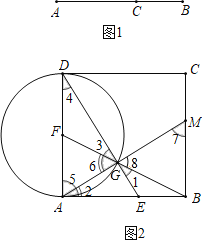
【题目】阅读下列材料,完成相应的学习任务:如图(1)在线段AB上找一点C,C把AB分为AC和BC两条线段,其中AC>BC.若AC,BC,AB满足关系AC2=BCAB.则点C叫做线段AB的黄金分割点,这时![]() =
=![]() ≈0.618,人们把
≈0.618,人们把![]() 叫做黄金分割数,我们可以根据图(2)所示操作方法我到线段AB的黄金分割点,操作步骤和部分证明过程如下:
叫做黄金分割数,我们可以根据图(2)所示操作方法我到线段AB的黄金分割点,操作步骤和部分证明过程如下:
第一步,以AB为边作正方形ABCD.
第二步,以AD为直径作⊙F.
第三步,连接BF与⊙F交于点G.
第四步,连接DG并延长与AB交于点E,则E就是线段AB的黄金分割点.
证明:连接AG并延长,与BC交于点M.
∵AD为⊙F的直径,
∴∠AGD=90°,
∵F为AD的中点,
∴DF=FG=AF,
∴∠3=∠4,∠5=∠6,
∵∠2+∠5=90°,∠5+∠4=90°,
∴∠2=∠4=∠3=∠1,
∵∠EBG=∠GBA,
∴△EBG∽△GBA,
∴![]() =
=![]() ,
,
∴BG2=BEAB…
任务:
(1)请根据上面操作步骤与部分证明过程,将剩余的证明过程补充完整;(提示:证明BM=BG=AE)
(2)优选法是一种具有广泛应用价值的数学方法,优选法中有一种0.618法应用了黄金分割数.为优选法的普及作出重要贡献的我国数学家是 (填出下列选项的字母代号)
A.华罗庚
B.陈景润
C.苏步青
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=4cm,若以点C为圆心,以2cm为半径作⊙C,则AB与⊙C的位置关系是( )
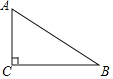
A.相离B.相切C.相交D.相切或相交
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,支付宝“集五福”活动中的“集五福”福卡共分为5种,分别为富强福、和谐福、友善福、爱国福、敬业福,从国家、社会和个人三个层面体现了社会主义核心价值观的价值目标.
(1)小明一家人春节期间参与了支付宝“集五福”活动,小明和姐姐都缺一个“敬业福”,恰巧爸爸有一个可以送给他们其中一个人,两个人各设计了一个游戏,获胜者得到“敬业福”.
在一个不透明盒子里放入标号分别为1,2,3,4的四个小球,这些小球除了标号数字外都相同,将小球摇匀.
小明的游戏规则是:从盒子中随机摸出一个小球,摸到标号数字为奇数小球,则判小明获胜,否则,判姐姐获胜.请判断,此游戏规则对小明和姐姐公平吗?说明理由.
姐姐的游戏规则是:小明从盒子中随机摸出一个小球,记下标号数字后放回盒里,充分摇匀后,姐姐再从盒中随机摸出一个小球,并记下标号数字.若两次摸到小球的标号数字同为奇数或同为偶数,则判小明获胜,若两次摸到小球的标号数字为一奇一偶,则判姐姐获胜.请用列表法或画树状图的方法进行判断此游戏规则对小明和姐姐是否公平.
(2)“五福”中体现了社会主义核心价值观的价值目标的个人层面有哪些?

查看答案和解析>>
科目:初中数学 来源: 题型:
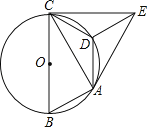
【题目】如图,已知⊙O是△ABC的外接圆,且BC为⊙O的直径,在劣弧![]() 上取一点D,使
上取一点D,使![]() ,将△ADC沿AD对折,得到△ADE,连接CE.
,将△ADC沿AD对折,得到△ADE,连接CE.
(1)求证:CE是⊙O的切线;
(2)若CE![]() C D,劣弧
C D,劣弧![]() 的弧长为π,求⊙O的半径.
的弧长为π,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
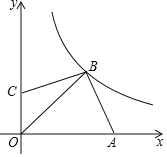
【题目】如图所示平面直角坐标系中,点A,C分别在x轴和y轴上,点B在第一象限,BC=BA,∠ABC=90°,反比例函数y=![]() .(x>0)的图象经过点B,若OB=2
.(x>0)的图象经过点B,若OB=2![]() ,则k的值为_____.
,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017四川省达州市,第10题,3分)已知函数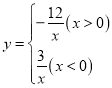 的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.下列结论:
的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.下列结论:
①若点M1(x1,y1),M2(x2,y2)在图象上,且x1<x2<0,则y1<y2;
②当点P坐标为(0,﹣3)时,△AOB是等腰三角形;
③无论点P在什么位置,始终有S△AOB=7.5,AP=4BP;
④当点P移动到使∠AOB=90°时,点A的坐标为(![]() ,
,![]() ).
).
其中正确的结论个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的过长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD、BC交于点F、E,连接AE.
(1)求证:AQ⊥DP;
(2)求证:AO2=ODOP;
(3)当BP=1时,求QO的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
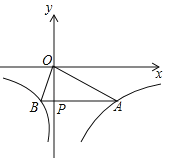
【题目】综合与实践—探究正方形旋转中的数学问题
问题情境:已知正方形![]() 中,点
中,点![]() 在
在![]() 边上,且
边上,且![]() .将正方形
.将正方形![]() 绕点
绕点![]() 顺时针旋转得到正方形
顺时针旋转得到正方形![]() (点
(点![]() ,
,![]() ,
,![]() ,
,![]() 分别是点
分别是点![]() ,
,![]() ,
,![]() ,
,![]() 的对应点).同学们通过小组合作,提出下列数学问题,请你解答.
的对应点).同学们通过小组合作,提出下列数学问题,请你解答.
特例分析:(1)“乐思”小组提出问题:如图1,当点![]() 落在正方形
落在正方形![]() 的对角线
的对角线![]() 上时,设线段
上时,设线段![]() 与
与![]() 交于点
交于点![]() .求证:四边形
.求证:四边形![]() 是矩形;
是矩形;
(2)“善学”小组提出问题:如图2,当线段![]() 经过点
经过点![]() 时,猜想线段
时,猜想线段![]() 与
与![]() 满足的数量关系,并说明理由;
满足的数量关系,并说明理由;
深入探究:(3)请从下面![]() ,
,![]() 两题中任选一题作答.我选择题.
两题中任选一题作答.我选择题.
A.在图2中连接![]() 和
和![]() ,请直接写出
,请直接写出![]() 的值.
的值.
B.“好问”小组提出问题:如图3,在正方形![]() 绕点
绕点![]() 顺时针旋转的过程中,设直线
顺时针旋转的过程中,设直线![]() 交线段
交线段![]() 于点
于点![]() .连接
.连接![]() ,并过点
,并过点![]() 作
作![]() 于点
于点![]() .请在图3中补全图形,并直接写出
.请在图3中补全图形,并直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
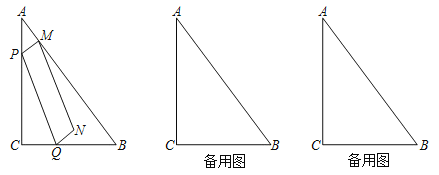
【题目】如图,已知在Rt△ABC中,∠C=90°,AC=8,BC=6,点P、Q分别在边AC、射线CB上,且AP=CQ,过点P作PM⊥AB,垂足为点M,联结PQ,以PM、PQ为邻边作平行四边形PQNM,设AP=x,平行四边形PQNM的面积为y.
(1)当平行四边形PQNM为矩形时,求∠PQM的正切值;
(2)当点N在△ABC内,求y关于x的函数解析式,并写出它的定义域;
(3)当过点P且平行于BC的直线经过平行四边形PQNM一边的中点时,直接写出x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com