
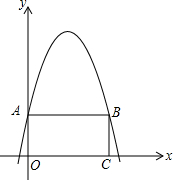
 如图,矩形AOCB的两边在坐标轴上,抛物线y=-x2+4x+2经过A、B两点.
如图,矩形AOCB的两边在坐标轴上,抛物线y=-x2+4x+2经过A、B两点.分析 (1)由抛物线的点的特点和矩形的性质,直接求出;
(2)①由运动特点分三种情况,用勾股定理计算即可;②当PQ∥OB时,时间t=$\frac{8}{7}$,再求出特殊位置的交点的横坐标,在判断出即可.
解答 解:(1)∵抛物线y=-x2+4x+2经过A、B两点,
∴A(0,2),
∵AB是矩形的一条边,
∴AB=4,
(2)Ⅰ、Q在AO边上,由运动有AP=t,AQ=4(t-1),
∴P(t,2),Q(0,6-4t),
∵C(4,0),
根据勾股定理得PQ2+PC2=CQ2,
∴t2+[4(t-1)]2+4+(4-t)2=16+(2-4(t-1))2,
∴t=-2+2$\sqrt{3}$,或t=-2-2$\sqrt{3}$(舍)
∴t=-2+2$\sqrt{3}$.
Ⅱ、Q在OC边上,AP=OQ,
∴4(t-1)-2=t.
∴t=2,
Ⅲ、Q在CB边上,同Ⅰ的方法得,t=3,
②当PQ∥OB时,
∴$\frac{CP}{CB}=\frac{CQ}{CO}$
∵P(t,2),Q(6-4t,0),
∴CP=6-t,CQ=4-(4t-2)=6-4t,
∴$\frac{6-t}{2}=\frac{6-4t}{4}$,
∴t=$\frac{8}{7}$,
∴点P的坐标为($\frac{8}{7}$,2);
由题意联立方程$\left\{\begin{array}{l}{y=\frac{7}{4}x}\\{y=-{x}^{2}+4x+2}\end{array}\right.$ 和$\left\{\begin{array}{l}{y=-\frac{7}{4}x}\\{y=-{x}^{2}+4x+2}\end{array}\right.$
∴x=$\frac{9±\sqrt{209}}{8}$和x=$\frac{23±3\sqrt{73}}{8}$,
∵∠POQ<∠HOQ
∴H点的取值范围为x<$\frac{23-3\sqrt{73}}{8}$和x>$\frac{9+\sqrt{209}}{8}$.
点评 此题是二次函数综合题,主要考查了勾股定理,矩形的性质,解本题的关键是用运动时间表示出线段.


 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
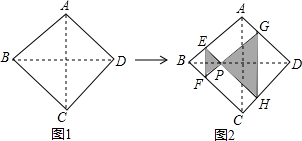
| A. | 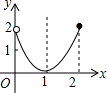 | B. | 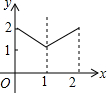 | C. | 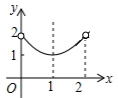 | D. | 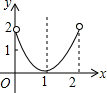 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3,1 | B. | 3,-1 | C. | -3,1 | D. | -3,-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com