
【题目】如图,割线ABC与⊙O相交于B、C两点,D为⊙O上一点,E为弧BC的中点,OE交BC于F,DE交AC于G,∠ADG=∠AGD.
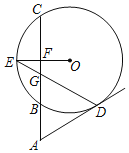
(1)求证明:AD是⊙D的切线;
(2)若∠A=60°,⊙O的半径为4,求ED的长.
【答案】(1)见解析;(2)DE=4![]() .
.
【解析】
(1)要证AD是⊙O的切线,只要连接OD,再证∠ADO=90°即可;
(2)作OH⊥ED于H,根据垂径定理得到DE=2DH,根据等边三角形的性质和直角三角形的性质即可得到结论.
(1)证明:连接OD.
∵E为BC的中点,
∴OE⊥BC,
∵OD=OE,
∴∠ODE=∠OED,
∴∠AGD +∠OED=∠EGF+∠OED=90°,
∵∠AGD=∠ADG,
∴∠ADG+∠ODE=90°,即OD⊥AD,
∴AD是⊙O的切线;
(2)作OH⊥ED于H,
∴DE=2DH,
∵∠ADG=∠AGD,
∴AG=AD,
∵∠A=60°,
∴∠ADG=60°,
∴∠ODE=30°,
∵OD=4,
∴DH=![]() OD=2
OD=2![]() ,
,
∴DE=2DH=4![]() .
.


科目:初中数学 来源: 题型:
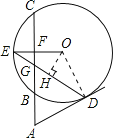
【题目】如图,一棵大树在一次强台风中折断倒下,未折断树杆![]() 与地面仍保持垂直的关系,而折断部分
与地面仍保持垂直的关系,而折断部分![]() 与未折断树杆
与未折断树杆![]() 形成
形成![]() 的夹角.树杆
的夹角.树杆![]() 旁有一座与地面垂直的铁塔
旁有一座与地面垂直的铁塔![]() ,测得
,测得![]() 米,塔高
米,塔高![]() 米.在某一时刻的太阳照射下,未折断树杆
米.在某一时刻的太阳照射下,未折断树杆![]() 落在地面的影子
落在地面的影子![]() 长为
长为![]() 米,且点
米,且点![]() 、
、![]() 、
、![]() 、
、![]() 在同一条直线上,点
在同一条直线上,点![]() 、
、![]() 、
、![]() 也在同一条直线上.求这棵大树没有折断前的高度.(结果精确到
也在同一条直线上.求这棵大树没有折断前的高度.(结果精确到![]() ,参考数据:
,参考数据: ![]() ,
, ![]() ,
, ![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于二次函数y=-x2-2x+3说法正确的是( )
A. 当![]() 时,函数最大值4
时,函数最大值4
B. 当![]() 时,函数最大值2
时,函数最大值2
C. 将其图象向上平移3个单位后,图象经过原点
D. 将其图象向左平移3个单位后,图象经过原点
查看答案和解析>>
科目:初中数学 来源: 题型:
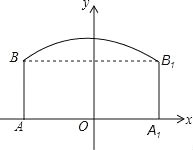
【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长为16m,宽为6m,抛物线的最高点C离地面AA1的距离为8m.
(1)按如图所示的直角坐标系,求表示该抛物线的函数表达式.
(2)一大型汽车装载某大型设备后,高为7m,宽为4m,如果该隧道内设双向行车道,那么这辆贷车能否安全通过?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到正方形
后得到正方形![]() ,依此方式,绕点
,依此方式,绕点![]() 连续旋转2019次得到正方形
连续旋转2019次得到正方形![]() ,如果点
,如果点![]() 的坐标为(1,0),那么点
的坐标为(1,0),那么点![]() 的坐标为________.
的坐标为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
尺规作图:过圆外一点作圆的切线.
已知:P为⊙O外一点.
求作:经过点P的⊙O的切线.
小敏的作法如下:
如图,
(1)连接OP,作线段OP的垂直平分线MN交OP于点C;
(2)以点C为圆心,CO的长为半径作圆,交⊙O于A,B两点;
(3)作直线PA,PB.所以直线PA,PB就是所求作的切线.
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是_____;由此可证明直线PA,PB都是⊙O的切线,其依据是_____.
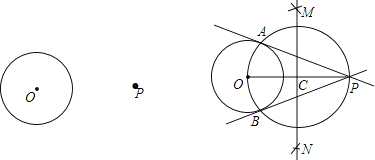
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+bx+c=0.
(1)若b=2m﹣1,m+c=﹣6,判断方程根的情况;
(2)若方程有两个相等的非零实数根,且b2﹣c2﹣4=0,求此时方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
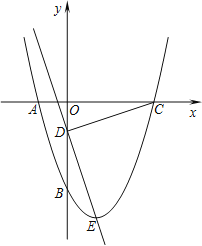
【题目】如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).
(1)求抛物线的函数解析式;
(2)点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;
(3)在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行了“禁毒知识竞赛”活动,并随即抽查了部分同学的成绩,整理并制作成图表如下:
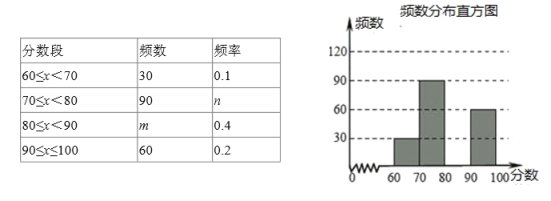
根据以上图表提供的信息,解答下列问题:
(1)请求出:![]() ,
,![]() ,抽查的总人数为 人;
,抽查的总人数为 人;
(2)请补全频数分布直方图;
(3)抽查成绩的中位数应落在 分数段内;
(4)如果比赛成绩在80分以上(含80分)为优秀,任意抽取一位同学,则成绩优秀的概率为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com