
【题目】在不透明的布袋中装有1个白球,2个红球,它们除颜色外其余完全相同.
(1)从袋中任意摸出两个球,试用树状图或表格列出所有等可能的结果,并求摸出的球恰好是两个红球的概率;
(2)若在布袋中再添加x个白球,充分搅匀,从中摸出一个球,使摸到白球的概率为 ![]() ,求添加的白球个数x.
,求添加的白球个数x.
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=45°,以AB为直径的⊙O交BC于点D,若BC=4 ![]() ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( ) 
A.π+1
B.π+2
C.2π+2
D.4π+1
查看答案和解析>>
科目:初中数学 来源: 题型:
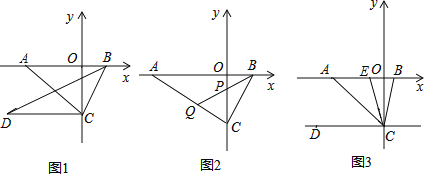
【题目】如图1,在平面直角坐标系中,点A为x轴负半轴上一点,点B为x轴正半轴上一点,![]() ,
,![]() ,其中a、b满足关系式:
,其中a、b满足关系式:![]() .
.
![]() ______,
______,![]() ______,
______,![]() 的面积为______;
的面积为______;
![]() 如图2,石
如图2,石![]() 于点C,点P是线段OC上一点,连接BP,延长BP交AC于点
于点C,点P是线段OC上一点,连接BP,延长BP交AC于点![]() 当
当![]() 时,求证:BP平分
时,求证:BP平分![]() ;
;![]() 提示:三角形三个内角和等于
提示:三角形三个内角和等于![]()
![]() 如图3,若
如图3,若![]() ,点E是点A与点B之间上一点连接CE,且CB平分
,点E是点A与点B之间上一点连接CE,且CB平分![]() 问
问![]() 与
与![]() 有什么数量关系?请写出它们之间的数量关系并请说明理由.
有什么数量关系?请写出它们之间的数量关系并请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:课外兴趣小组活动时,老师提出了如下问题:
如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(1)问题解决:受到(1)的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明;
(2)问题拓展:如图3,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,联结EF、CF,那么下列结论①∠DCF=![]() ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序号).
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序号).


图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个圆柱的底面半径是10 cm,高是18 cm,把这个圆柱放在水平桌面上,如图所示.
(1)如果用一个平面沿水平方向去截这个圆柱,所得的截面是什么形状?
(2)如果用一个平面沿竖直方向去截这个圆柱,所得的截面是什么形状?
(3)怎样截时所得的截面是长方形且长方形的面积最大,请你画出这个截面并求其面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
探究1:如图l,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90![]() +
+![]() ∠A,理由如下:
∠A,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线
∴∠1=![]() ∠ABC, ∠2=
∠ABC, ∠2=![]() ∠ACB
∠ACB
∴∠l+∠2=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180
(180![]() -∠A)= 90
-∠A)= 90![]() -
-![]() ∠A
∠A
∴∠BOC=180![]() -(∠1+∠2) =180
-(∠1+∠2) =180![]() -(90
-(90![]() -
-![]() ∠A)=90
∠A)=90![]() +
+![]() ∠A
∠A
(1)探究2;如图2中,O是![]() ∠ABC与外角
∠ABC与外角![]() ∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
(2)探究3:如图3中, O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(直接写出结论)
(3)拓展:如图4,在四边形ABCD中,O是∠ABC与∠DCB的平分线BO和CO的交点,则∠BOC与∠A+∠D有怎样的关系?(直接写出结论)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿射线AC的方向匀速平移得到△PNM,速度为1cm/s,同时,点Q从点C出发,沿射线CB方向匀速运动,速度为1cm/s,当△PNM停止平移时,点Q也停止运动,如图2所示,设运动时间为t(s)(0<t<4).
(1)当t为何值时,PQ∥MN?
(2)设△QMC的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使得PQ=QM,若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式ax5+bx3+3x+c,当x=0时,该代数式的值为﹣1.
(1)求c的值;
(2)已知当x=3时,该式子的值为9,试求当x=﹣3时该式子的值;
(3)在第(2)小题的已知条件下,若有3a=5b成立,试比较a+b与c的大小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com