
如图1,边长为4的正方形ABCD中,点E在AB边上(不与点A、B重合),点F在BC边上(不与点B、C重合)。
第一次操作:将线段EF绕点F顺时针旋转,当点E落在正方形上时,记为点G;
第二次操作:将线段FG绕点G顺时针旋转,当点F落在正方形上时,记为点H;
依此操作下去…

(1)图2中的三角形EFD是经过两次操作后得到的,其形状为____,求此时线段EF的长;
(2)若经过三次操作可得到四边形EFGH。
①请判断四边形EFGH的形状为______,此时AE与BF的数量关系是______。
②以①中的结论为前提,设AE的长为x,四边形EFGH的面积为y,求y与x的函数关系式及面积y的取值范围。
【解答】(1)等边三角.
∵四边形ABCD是正方形,
 ∴AD=CD=BC=AB,∠A=∠B=∠C=90°.
∴AD=CD=BC=AB,∠A=∠B=∠C=90°.
∵ED=FD,
∴△ADE≌△CDF.(HL)
∴AE=CF,BE=BF.
∴BEF是等腰直角三角形。
设BE的长为x,则EF=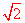 x,AE=4- x.
x,AE=4- x.
∵在Rt△AED中, ,DE=EF,
,DE=EF,
∴
解得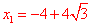 ,
,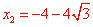 (不合题意,舍去).
(不合题意,舍去).
∴EF=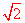 x=
x=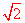 (-
(-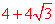 )=-4+4
)=-4+4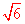
(2) ①四边形EFGH为正方形;AE=BF.
②∵AE=x,
∴BE=4-x.
 ∵在Rt△BED中,
∵在Rt△BED中, ,AE=BF,
,AE=BF,
∴
∵点E不与点A、B重合,点F不与点B、C重合,
∴0<x<4.
∵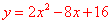
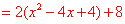
 ,
,
∴当x=2时有最小值8,当x=0或4时,有最大值16,
∴y的取值范围是8<y<16.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
如图,在四边行ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.
(1)求证:四边形ABEF是菱形;
(2)若AE= 6,BF = 8,CE = 3,求四边行ABCD的面积.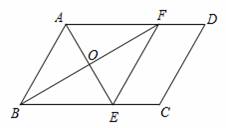
查看答案和解析>>
科目:初中数学 来源: 题型:
某教研机构为了解在校初中生阅读数学教科书的现状,随机抽取某部分初中学生进行了调查。依据相关数据绘制成以下不完整的统计图表,请根据图表中的信息解答下列问题:
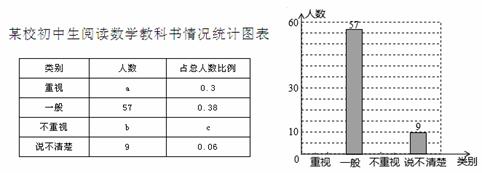
(1)求样本容量及表格中a、b、c的值,并补全统计图;
(2)若该校共有初中生2300名,请估计该校“不重视阅读教科书”的初中生人数
(3)①根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;
查看答案和解析>>
科目:初中数学 来源: 题型:
从 A 地向 B 地打长途电话,通话时间不超过 3min 收费 2.4 元,超过 3min 后每分加收1 元.
(Ⅰ)根据题意,填写下表:

(Ⅱ)设通话时间为 x min,通话费用 y 元,求 y 与 x 的函数解析式;
(Ⅲ)若小红有 10 元钱,求她打一次电话最多可以通话的时间(本题中通话时间取整数,不足 1min 的通话时间按 1min 计费).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com