
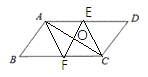
【题目】如图,要在平行四边形![]() 内作一个菱形.甲,乙两位同学的作法分别如下:
内作一个菱形.甲,乙两位同学的作法分别如下:

对于甲乙两人的作法,可判断( )
A.甲正确,乙错误B.甲错误,乙正确C.甲,乙均正确D.甲、乙均错误
【答案】C
【解析】
甲:首先证明△AOE≌△COF(ASA),可得AE=CF,再根据一组对边平行且相等的四边形是平行四边形可判定四边形AECF是平行四边形,再由AC⊥EF,可根据对角线互相垂直的四边形是菱形判定出AECF是菱形;乙:四边形ABCD是平行四边形,可根据角平分线的定义和平行线的定义,求得AB=AF,所以四边形ABEF是菱形.
甲的作法正确,
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵EF是AC的垂直平分线,
∴AO=CO,
在△AOE和△COF中,
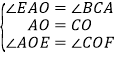 ,
,
∴△AOE≌△COF(ASA),
∴AE=CF,
又∵AE∥CF,
∴四边形AFCE是平行四边形,
∵EF⊥AC,
∴四边形AFCE是菱形;
乙的作法正确;
证明:∵AD∥BC,

∴∠1=∠2,∠6=∠7,
∵BF平分∠ABC,AE平分∠BAD,
∴∠2=∠3,∠5=∠6,
∴∠1=∠3,∠5=∠7,
∴AB=AF,AB=BE,
∴AF=BE,
∵AF∥BE,且AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴平行四边形ABEF是菱形;
故甲、乙做法均正确.
故选C.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是 . 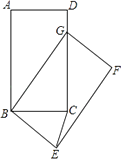
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M是正方形ABCD的边BC上一点,连接AM,点E是线段AM上一点,∠CDE的平分线交AM延长线于点F.
(1)如图1,若点E为线段AM的中点,BM:CM=1:2,BE=![]() ,求AB的长;
,求AB的长;
(2)如图2,若DA=DE,求证:BF+DF=![]() AF.
AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
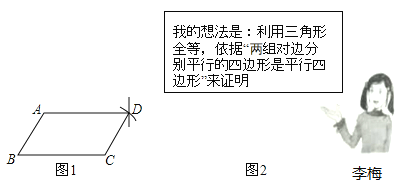
【题目】李梅同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形![]() ,并写出了如下不完整的已知和求证.
,并写出了如下不完整的已知和求证.
已知:如图1,在四边形![]() 中,
中,![]() ,
,![]()
求证:四边形![]() 是 四边形.
是 四边形.
(1)填空,补全已知和求证;
(2)按李梅的想法写出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料130kg,乙种原料144kg.现用这两种原料生产出A,B两种产品共30件.已知生产每件A产品需甲种原料5kg,乙种原料4kg,且每件A产品可获利700元;生产每件B产品需甲种原料3kg,乙种原料6kg,且每件B产品可获利900元.设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种;
(2)设生产这30件产品可获利y元,写出y关于x的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D ,点E为线段BC的中点,AD=2,tan A=2.
(1)求AB的长;
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1 . 
(1)在图中画出△A1B1C1;
(2)点A1 , B1 , C1的坐标分别为、、;
(3)若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com