
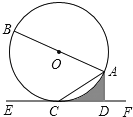
【题目】如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
(1)求证:EF是⊙O的切线;
(2)求证:AC2=ADAB.
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三个顶点和点O都在正方形网格的格点上,每个小正方形的边长都为1.
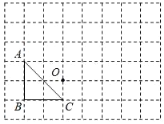
(1)将△ABC先向右平移4个单位,再向上平移2个单位得到△A1B1C1,请画出△A1B1C1;
(2)请画出△A2B2C2,使△A2B2C2和△ABC关于点O成中心对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
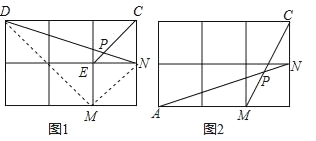
【题目】(问题呈现)如图1,在边长为1的正方形网格中,连接格点D,N和E,C,DN和EC相交于点P,求tan∠CPN的值.
(方法归纳)求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中∠CPN不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点M,N,可得MN∥EC,则∠DNM=∠CPN,连接DM,那么∠CPN就变换到Rt△DMN中.
(问题解决)(1)直接写出图1中tan∠CPN的值为 ;
(2)如图2,在边长为1的正方形网格中,AN与CM相交于点P,求cos∠CPN的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
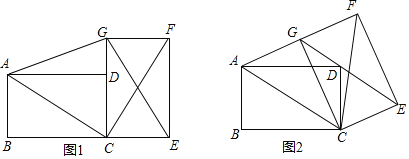
【题目】两张矩形纸片ABCD和CEFG完全相同,且AB=CE,AD>AB.
操作发现:
(1)如图1,点D在GC上,连接AC、CF、CG、AG,则AC和CF有何数量关系和位置关系?并说明理由.
实践探究:
(2)如图2,将图1中的纸片CEFG以点C为旋转中心逆时针旋转,当点D落在GE上时停止旋转,则AG和GF在同一条直线上吗?请判断,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商销售一种成本价为10元/kg的商品,已知销售价不低于成本价,且物价部门规定这种产品的销售价不得高于18元/kg.在销售过程中发现销量y(kg)与售价x(元/kg)之间满足一次函数关系,对应关系如下表所示:
x | 12 | 14 | 15 | 17 |
y | 36 | 32 | 30 | 26 |
⑴求y与x之间的函数关系式,并写出自变量x的取值范围;
⑵若该经销商想使这种商品获得平均每天168元的利润,求售价应定为多少元/kg?
⑶设销售这种商品每天所获得的利润为W元,求W与x之间的函数关系式;并求出该商品销售单价定为多少元时,才能使经销商所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于自变量为![]() 的函数,当
的函数,当![]() 时,其函数值也为
时,其函数值也为![]() ,则称点
,则称点![]() 为此函数的不动点.若函数
为此函数的不动点.若函数![]() 图象上有两个不动点
图象上有两个不动点![]() 、
、![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,
,![]() ,求函数
,求函数![]() 的不动点坐标;
的不动点坐标;
(2)求证;![]() ;
;
(3)若函数![]() ,
,![]() ,
,![]() ,当
,当![]() 时,
时,
①求证:![]() ;
;
②求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
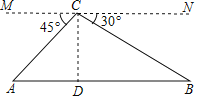
【题目】如图,某景区的两个景点A、B处于同一水平地面上、一架无人机在空中沿MN方向水平飞行进行航拍作业,MN与AB在同一铅直平面内,当无人机飞行至C处时、测得景点A的俯角为45°,景点B的俯角为30°,此时C到地面的距离CD为100米,则两景点A、B间的距离为__米(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com