
【题目】已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?
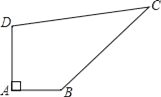
【答案】7200元
【解析】试题分析:仔细分析题目,需要求得四边形的面积才能求得结果.连接BD,在直角三角形ABD中可求得BD的长,由BD、CD、BC的长度关系可得三角形DBC为一直角三角形,DC为斜边;由此看,四边形ABCD由Rt△ABD和Rt△DBC构成,则容易求解.
试题解析:连接BD,
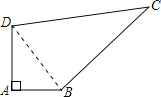
在Rt△ABD中,BD2=AB2+AD2=32+42=52,
在△CBD中,CD2=132BC2=122,
而122+52=132,
即BC2+BD2=CD2,
∴∠DBC=90°,
S四边形ABCD=S△BAD+S△DBC=![]() ADAB+
ADAB+![]() DBBC,
DBBC,
=![]() ×4×3+
×4×3+![]() ×12×5=36.
×12×5=36.
所以需费用36×200=7200(元).


科目:初中数学 来源: 题型:
【题目】如图,C为线段AB延长线上一点,D为线段BC上一点,CD=2BD,E为线段AC上一点,CE=2AE
![]()
(1)若AB=18,BC=21,求DE的长;
(2)若AB=a,求DE的长;(用含a的代数式表示)
(3)若图中所有线段的长度之和是线段AD长度的7倍,则![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)-24×![]() ;
;
(2)-9+5×(-6)-(-4)2÷(-8);
(3)0.25×(-2)2-[4÷![]() +1]+(-1)2018;
+1]+(-1)2018;
(4)-42÷![]() -[
-[![]() ].
].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图17-Z-10是由边长为1的小正方形组成的网格.
(1)求四边形ABCD的面积;
(2)你能判断AD与CD的位置关系吗?说出你的理由.

图17-Z-10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10 cm,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1cm的速度运动,同时点Q从点C出发沿射线CB方向以每秒2cm的速度运动,在线段QC上取点E,使得QE =2cm,连结PE,设点P的运动时间为t秒.
(1)若PE⊥BC,则①PE= cm,CE= (用含t的式子表示);
②求BQ的长;
(2)请问是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠A+∠D=180°,∠1=3∠2,∠2=24°,点P是BC上的一点.
(1)请写出图中∠1的一对同位角,一对内错角,一对同旁内角;
(2)求∠EFC与∠E的度数;
(3)若∠BFP=46°,请判断CE与PF是否平行?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=

求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线AC上,点A′落在CD的延长线上),A′B′交AD于点E,连接AA′、CE.
求证: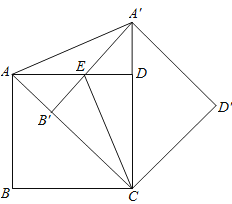
(1)△ADA′≌△CDE;
(2)直线CE是线段AA′的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com