
【题目】如图,在直角梯形ABCD中,AD∥BC,∠B=90°,E为AB上一点,且ED平分∠ADC,EC平分∠BCD,则下列结论中错误的是( )

A. AE=BE B. DE⊥CE C. CD=AD+BC D. CD=AD+CE
【答案】D
【解析】
根据直角梯形、等腰三角形的判定与性质以及全等三角形的判定与性质进行分析、 判断,可得正确的选择.
解:B,![]() AD//BC,
AD//BC,![]() ∠ADC+∠BCD=180,
∠ADC+∠BCD=180,
![]() ED平分∠ADC,EC平分∠BCD,
ED平分∠ADC,EC平分∠BCD,
![]() ∠EDC=
∠EDC=![]() ∠ADC, ∠DCE=
∠ADC, ∠DCE=![]() ∠DCB,
∠DCB,
![]() ∠EDC+∠DCE=
∠EDC+∠DCE=![]()
![]() 180
180![]() =90
=90![]() ,
,
![]() ∠DEC=180
∠DEC=180![]() -90
-90![]() =90
=90![]() ,
,
故B选项不符合题意;
A、C选项,延长DE交CB的延长线于点F. 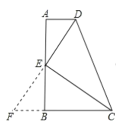
![]() AD//BC, DE是∠ADC的角平分线,
AD//BC, DE是∠ADC的角平分线,
![]() ∠CDF=∠ADE=∠DFC ,
∠CDF=∠ADE=∠DFC ,
![]() CD=CF,
CD=CF,
![]() △CDF 是等腰三角形;
△CDF 是等腰三角形;
又由前面得DE⊥EC,
![]() DE=FE,
DE=FE,
又![]() ∠AED=∠BEF,
∠AED=∠BEF,
![]() △BEF≌△AED,
△BEF≌△AED,
![]() AE=EB,
AE=EB,
故A选项不符合题意;
![]() AD=BF,又
AD=BF,又![]() CD=CF,
CD=CF,
![]() CD=CF=BC+BF=AD+BC,
CD=CF=BC+BF=AD+BC,
故C选项不符合题意,
无法得出D选项,
故本题答案:D


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.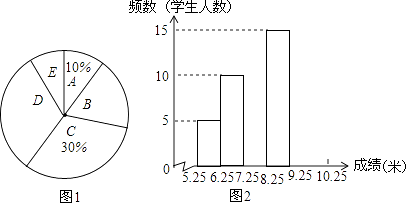
(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】常用的分解因式的方法有提取公因式法、公式法,但有更多的多项式只用上述方法就无法分解,如x2﹣4y2﹣2x+4y,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了,过程为:x2﹣4y2﹣2x+4y=(x+2y)(x﹣2y)﹣2(x﹣2y)=(x﹣2y)(x+2y﹣2),这种分解因式的方法叫分组分解法,利用这种方法解决下列问题.
(1)分解因式:x2+2xy+y2;
(2)分解因式:a2﹣9﹣2ab+b2;
(3)△ABC三边a、b、c满足a2﹣4bc+4ac﹣ab=0,判断△ABC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 分别在线段
分别在线段![]() 上,
上,![]() 交
交![]() 于点
于点![]() 平分
平分![]() .
.
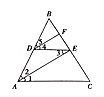
(1)求证:![]() 平分
平分![]() 阅读下列推理过程,并将推理过程补充完整.
阅读下列推理过程,并将推理过程补充完整.
证明:![]() 平分
平分![]() ,(已知)
,(已知)
![]() (角平分线的定义)
(角平分线的定义)
![]() ,(已知)
,(已知)
![]() ( )
( )
故 .(等量代换)
![]() ,(已知)
,(已知)
![]() ,( )
,( )
![]() ,( )
,( )
![]() ,
,
![]() 平分
平分![]() .( )
.( )
(2)若![]() ,请直接写出图中所有与
,请直接写出图中所有与![]() 互余的角.
互余的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AB=4,角BAC的平分线交BC于点D,M为AB边中点,N是AD上的动点.
①在图上作出使得BN+MN的和最小时点N的位置,并说明理由.
②求出BN+MN的最小值.(提示:Rt△ABC中,∠C=90°,则有AC2+BC2=AB2成立)
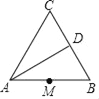
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某体育用品商店,购买50根跳绳和80个毽子共用1120元,购买30根跳绳和50个毽子共用680元.
(1)跳绳、毽子的单价各是多少元?
(2)该店在“元旦”节期间开展促销活动,所有商品按同样的折数打折销售.节日期间购买100根跳绳和100个毽子只需1700元,该店的商品按原价的几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,F分别是矩形ABCD的边BC和CD上的点,其中AB=3 ![]() ,BC=3
,BC=3 ![]() ,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为 .
,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为 . 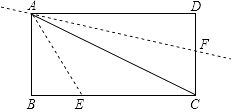
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com