
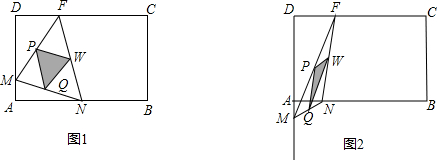
 ∴4-x=2x,
∴4-x=2x,| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
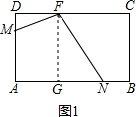
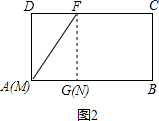
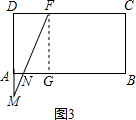 (3)①当0≤x≤4,即M从D到A运动时,只有当x=4时,MN的值最小,等于2;
(3)①当0≤x≤4,即M从D到A运动时,只有当x=4时,MN的值最小,等于2;| 2 |
| 2 |


科目:初中数学 来源:不详 题型:单选题
| A.向上平移4个单位 | B.向下平移4个单位 |
| C.向左平移4个单位 | D.向右平移4个单位 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
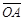 =10, ÐAOB=36°。若固定B点,将此扇形依顺时针方向旋转,得一新扇形A’O’B,其中A点在
=10, ÐAOB=36°。若固定B点,将此扇形依顺时针方向旋转,得一新扇形A’O’B,其中A点在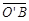 上,如图(十四)所示,则O点旋转至O’点所经过的轨迹长度为何?
上,如图(十四)所示,则O点旋转至O’点所经过的轨迹长度为何?
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.∠A+∠B=∠C | B.∠A:∠B:∠C=1:2:3 |
| C.a2=c2-b2 | D.a:b:c=3:4:6 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
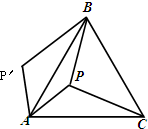
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.锐角三角形 |
| B.直角三角形 |
| C.钝角三角形 |
| D.锐角三角形或钝角三角形 |
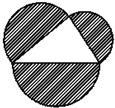
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com