练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

     在正方形网格中，△ABC的位置如图所示，则sin B的值是

    A.         B．       C．        D．


    A

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，在等腰直角中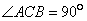，，O是斜边AB的中点，点D、E分别在直角边AC、BC上，且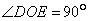，DE交OC于点P．则下列结论：

    （1）图形中全等的三角形只有两对；

    （2）的面积等于四边形CDOE面积的2倍；

    （3）；

    （4）．其中正确的结论有（　　）

     

       A．1个       B．2个        C．3个       D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    四边形ABCD中，E是边AB上一点（不与点A，B重合），连接ED，EC，则将四

    边形ABCD分成三个三角形．若其中有两个三角形相似，则把E叫做四边形ABCD

    的边AB上的相似点；若这三个三角形都相似，则把E叫做四边形ABCD的边AB上

    的黄金相似点．

    （1）如图①，∠A=∠B=∠DEC=60°，试判断点E是否为四边形ABCD的边AB上的

    相似点？并说明理由；

    （2）如图②，在（1）的条件下，若E是AB的中点，

    ①判断点E是否为四边形ABCD的边AB上的黄金相似点？并说明理由；

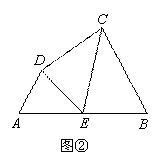    ②若AD·BC=18，求AB的长；

    （3）在矩形ABCD中，AB=10，BC=3，且A，B，C，D四点均在正方形网格（网格

    中每个小正方形的边长为1）的格点上，试在图③中画出矩形ABCD的边AB上

    的一个黄金相似点E．

                                                                                                             

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知：如图，在中，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图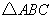，和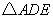都是以A为直角顶点的等腰直角三角形，连结BD，BE，CE，延长CE交AB于点F，交BD于点G．

    （1）求证：；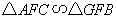

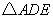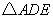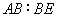    （2）若是边长可变化的等腰直角三角形，并将绕点旋转，使CE的延长线始终与线段BD（包括端点B、D）相交．当为等腰直角三角形时，求出的值．

                            

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如果两个相似三角形的相似比是2:3，那么它们的周长比是        ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    （1） △AEB ∽ △CBA .

    （或△AEB∽△BFC；△AEB∽△ADC；△CAB∽△BFC；△BFC∽△ADC . ）

    证明：∵四边形ABCD和四边形AEFC是矩形，

    ∴∠E =∠CBA=∠EAC=90°.

    ∵∠EAB+∠CAB=90°，

    ∠EAB+∠ABE=90°，

    ∴∠ABE=∠CAB.

    ∴△AEB ∽ △CBA.

    （2）解：∵△AEB ∽ △CBA，

    ∴ . ∴.

    ∵

    ∴.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若“Δ”是新规定的某种运算符号，设xΔy＝xy＋x＋y，则2Δm＝－16中，m的值为(　　)．

    A．8            B．－8          C．6            D．－6

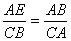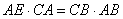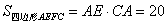    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若a＋b＞0，且b＜0，则a，b，－a，－b的大小关系为(　　)．

    A．－a＜－b＜b＜a               B．－a＜b＜－b＜a

    C．－a＜b＜a＜－b               D．b＜－a＜－b＜a

    查看答案和解析>>

    同步练习册答案