
(本小题满分9分)
已知:△ABC是任意三角形.
⑴如图1所示,点M、P、N分别是边AB、BC、CA的中点.求证:∠MPN=∠A.
⑵如图2所示,点M、N分别在边AB、AC上,且,
,点P1、P2是边BC的三等分点,你认为∠MP1N+∠MP2N=∠A是否正确?请说明你的理由.
⑶如图3所示,点M、N分别在边AB、AC上,且,
,点P1、P2、……、P2009是边BC的2010等分点,则∠MP1N+∠MP2N+……+∠MP2009N=____________.
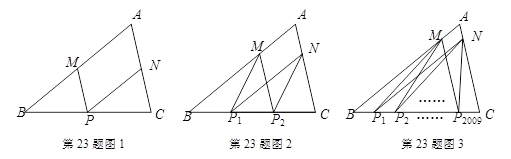
(请直接将该小问的答案写在横线上.)
(1)略
(2)正确
(3)∠A
解析:⑴证明:∵点M、P、N分别是AB、BC、CA的中点,
∴线段MP、PN是△ABC的中位线,
∴MP∥AN,PN∥AM, 1分
∴四边形AMPN是平行四边形, 2分
∴∠MPN=∠A. 3分
⑵∠MP1N+∠MP2N=∠A正确. 4分
如图所示,连接MN, 5分
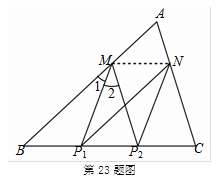
∵,∠A=∠A,
∴△AMN∽△ABC,
∴∠AMN=∠B,,
∴MN∥BC,MN=BC, 6分
∵点P1、P2是边BC的三等分点,
∴MN与BP1平行且相等,MN与P1P2平行且相等,MN与P2C平行且相等,
∴四边形MBP1N、MP1P2N、MP2CN都是平行四边形,
∴MB∥NP1,MP1∥NP2,MP2∥AC,
7分
∴∠MP1N=∠1,∠MP2N=∠2,∠BMP2=∠A,
∴∠MP1N+∠MP2N=∠1+∠2=∠BMP2=∠A.
8分
⑶∠A. 9分


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:



查看答案和解析>>
科目:初中数学 来源: 题型:
 经过点M(2,1),且与x轴交于点A,与y轴交于点B.
经过点M(2,1),且与x轴交于点A,与y轴交于点B.
查看答案和解析>>
科目:初中数学 来源: 题型:
 与y轴交于点C(0,
与y轴交于点C(0, ), 与x轴交于点A、 B,点A的坐标为(2,0).
), 与x轴交于点A、 B,点A的坐标为(2,0).
 与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为(
与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为( ,0).问:是否存在这样的直线
,0).问:是否存在这样的直线 ,使得△OMF是等腰三角形?若存 在,请求出点Q的坐标;若不存在,请说明理由.
,使得△OMF是等腰三角形?若存 在,请求出点Q的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:2010-2011学年河南省周口市初三下学期第二十七章相似三角形检测题 题型:解答题
(本小题满分7分)
已知:关于 的一元二次方程
的一元二次方程 .
.
(1)若方程有两个不相等的实数根,求 的取值范围;
的取值范围;
(2)在(1)的条件下,求证:无论 取何值,抛物线y=
取何值,抛物线y= 总过
总过 轴上的一个固定点;
轴上的一个固定点;
(3)若 为正整数,且关于
为正整数,且关于 的一元二次方程
的一元二次方程 有两个不相等的整数根,把抛物线y=
有两个不相等的整数根,把抛物线y= 向右平移4个单位长度,求平移后的抛物线的解析式.
向右平移4个单位长度,求平移后的抛物线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com