
【题目】如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G、F两点.
(1)求证:AB与⊙O相切;
(2)若等边三角形ABC的边长是8,求线段BF的长.

【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)过点O作OM⊥AB,垂足是M,证明OM等于圆的半径OD即可;
(2)过点O作ON⊥BE,垂足是N,连接OF,则四边形OMBN是矩形,在直角△OBM利用三角函数求得OM和BM的长,则BN和ON即可求得,在直角△ONF中利用勾股定理求得NF,则BF即可求解.
试题解析:(1)过点O作OM⊥AB,垂足是M ,
∵⊙O与AC相切于点D ,∴OD⊥AC ,∴∠ADO=∠AMO=90°,
∵△ABC是等边三角形, AO⊥BC,∴OA是∠MAD的角平分线,
∵OD⊥AC,OM⊥AB,∴OM=OD ,
∴AB与⊙O相切;
(2)过点O作ON⊥BE,垂足是N,连接OF ,
∵AB=AC,AO⊥BC ,
∴O是BC的中点,
∴![]() ,
,
在直角△ABC中,∠ABE=90°,∠MBO=60°,
∴∠OBN=30° ,
∵ON⊥BE,∠OBN=30°,OB=4,
∴![]() ,
, ![]() ,
,
∵AB⊥BE,
∴四边形OMBN是矩形,
∴![]() ,
,
∵![]() ,
,
由勾股定理得![]() ,
,
∴![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角板的直角顶点![]() 按如图方式叠放在一起,友情提示:
按如图方式叠放在一起,友情提示:![]() ,
,![]() ,
,![]() .
.
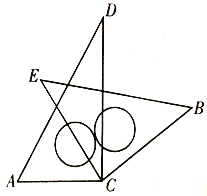
(1)①若![]() ,则
,则![]() 的度数为__________;
的度数为__________;
②若![]() ,则
,则![]() 的度数为__________.
的度数为__________.
(2)由(1)猜想![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)当![]() 且点
且点![]() 在直线
在直线![]() 的上方时,当这两块角尺有一组边互相平行时,请直接写出
的上方时,当这两块角尺有一组边互相平行时,请直接写出![]() 角度所有可能的值.
角度所有可能的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
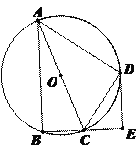
【题目】如图,四边形ABCD是⊙O的内接四边形, ![]() ,AC为直径, DE⊥BC,垂足为E.
,AC为直径, DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)若AC=9,CE=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(方法回顾)证明:三角形中位线定理.
已知:如图1,![]() 中,D、E分别是AB、AC的中点.
中,D、E分别是AB、AC的中点.
求证:![]() ,
,![]() .
.
证明:如图1,延长DE到点F,使得![]() ,连接CF;
,连接CF;
请继续完成证明过程;

(2)(问题解决)
如图2,在矩形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若![]() ,
,![]() ,
,![]() ,求GF的长.
,求GF的长.
(3)(思维拓展)
如图3,在梯形ABCD中,![]() ,
,![]() ,
,![]() ,E为AD的中点,G、F分别为AB、CD边上的点,若
,E为AD的中点,G、F分别为AB、CD边上的点,若![]() ,
,![]() ,
,![]() ,求GF的长.
,求GF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
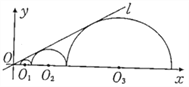
【题目】如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆On均与直线l相切,设半圆O1,半圆O2,…,半圆On的半径分别是r1,r2,…,rn,则当直线l与x轴所成锐角为30![]() 时,且r1=1时,r2017=_______.
时,且r1=1时,r2017=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个长方形运动场被分隔成A,B,A,B,C共5个区,A区是边长为a m的正方形,C区是边长为c m的正方形.
(1)列式表示每个B区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果a=40,c=10,求整个长方形运动场的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一条直线过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() 两点,其中点
两点,其中点![]() 的横坐标是
的横坐标是![]() .
.
⑴求这条直线的函数关系式及点![]() 的坐标 ;
的坐标 ;
⑵在![]() 轴上是否存在点
轴上是否存在点![]() ,使得△
,使得△![]() 是直角三角形?若存在,求出点
是直角三角形?若存在,求出点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
⑶过线段![]() 上一点
上一点![]() ,作
,作![]() ∥
∥![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,点
,点![]() 在第一象限;点
在第一象限;点![]() ,当点
,当点![]() 的横坐标为何值时,
的横坐标为何值时, ![]() 的长度最大?最大值是多少?
的长度最大?最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,
,![]() .把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是__________.
.把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com