
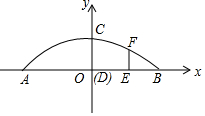
 某地欲搭建一桥,桥的底部两端间的距离AB=L,称跨度,桥面最高点到AB的距离CD=h称拱高,当L和h确定时,有两种设计方案可供选择:①抛物线型,②圆弧型.已知这座桥的跨度L=32米,拱高h=8米.
某地欲搭建一桥,桥的底部两端间的距离AB=L,称跨度,桥面最高点到AB的距离CD=h称拱高,当L和h确定时,有两种设计方案可供选择:①抛物线型,②圆弧型.已知这座桥的跨度L=32米,拱高h=8米.分析 (1)抛物线的解析式为y=ax2+c,把点C(0,8)和点B(16,0),代入即可求出抛物线解析式;
(2)设弧AB所在的圆心为O,C为弧AB的中点,CD⊥AB于D,延长CD经过O点,设⊙O的半径为R,利用勾股定理求出即可;
(3)根据题意画出图形,利用垂径定理以及勾股定理得出AO的长,再求出EF的长即可.
解答 解:(1)抛物线的解析式为y=ax2+c,
又∵抛物线经过点C(0,8)和点B(16,0),
∴0=256a+8,a=-$\frac{1}{32}$.
∴抛物线的解析式为y=-$\frac{1}{32}$x2+8(-16≤x≤16);
(2)设弧AB所在的圆心为O,C为弧AB的中点,CD⊥AB于D,延长CD经过O点,设⊙O的半径为R,
在Rt△OBD中,OB2=OD2+DB2
∴R2=(R-8)2+162,解得R=20;
(3)①在抛物线型中设点F(x,y)在抛物线上,x=OE=16-4=12,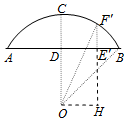
EF=y=3.5米;
②在圆弧型中设点F′在弧AB上,作F′E′⊥AB于E′,
OH⊥F′E′于H,则OH=D E′=16-4=12,O F′=R=20,
在Rt△OH F′中,H F′=$\sqrt{2{0}^{2}-1{2}^{2}}$,
∵HE′=OD=OC-CD=20-8=12,E′F′=HF′-HE′=16-12=4(米)
∴在离桥的一端4米处,抛物线型桥墩高3.5米; 圆弧型桥墩高4米.
点评 此题主要考查了垂径定理的应用以及二次函数的应用,根据题意画出图形结合勾股定理得出是解题关键.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{12}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
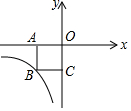 如图,正方形OABC的面积是4,点B在反比例函数y=$\frac{k}{x}$(x<0)的图象上.则反比例函数的解析式是( )
如图,正方形OABC的面积是4,点B在反比例函数y=$\frac{k}{x}$(x<0)的图象上.则反比例函数的解析式是( )| A. | y=$\frac{4}{x}$ | B. | y=$\frac{2}{x}$ | C. | y=-$\frac{2}{x}$ | D. | y=-$\frac{4}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
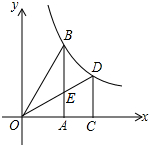 如图,B、D是反比例函数y=$\frac{k}{x}$图象上两点,过B,D作x轴的垂线,垂足分别为A,C,连接OD交AB于点E,若∠ABO=30°,OD是∠BOA的平分线,四边形ACDE的面积为2,则k=6.
如图,B、D是反比例函数y=$\frac{k}{x}$图象上两点,过B,D作x轴的垂线,垂足分别为A,C,连接OD交AB于点E,若∠ABO=30°,OD是∠BOA的平分线,四边形ACDE的面积为2,则k=6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com