
����Ŀ��ǭ������ijУ����ʦ��֯�ţ�1����ͬѧ��չ��ѧ�������ͬѧ�Dz���ѧУ����һ���߸˵ĸߣ���֪���߸�ֱ���ڵ����ϣ�ij����̫����������£����߸˵�Ӱ�ӣ�����BCD��ǡ������ˮƽ�����б���ϣ���D����õ��߸˶���A������Ϊ30�㣬��C����õ��߸˶���A������Ϊ45�㣬б��������60��ǣ�CD=4m�����������Щ��������߸˵ĸߣ�AB����
�������ȷ��1m���ο����ݣ� ![]() ��1.4��
��1.4�� ![]() ��1.7��
��1.7��
���𰸡��⣺�ӳ�AD��BC���ӳ�����G����DH��BG��H����ͼ��ʾ��
��Rt��DHC�У���DCH=60�㣬CD=4��
��CH=CDcos��DCH=4��cos60��=2��DH=CDsin��DCH=4��sin60��=2 ![]() ��
��
��DH��BG����G=30�㣬
��HG= ![]() =
= ![]() =6��
=6��
��CG=CH+HG=2+6=8��
��AB=xm��
��AB��BG����G=30�㣬��BCA=45�㣬
��BC=x��BG= ![]() =
= ![]() =
= ![]() x��
x��
��BG��BC=CG��
�� ![]() x��x=8��
x��x=8��
��ã�x��11��m����
�𣺵��߸˵ĸ�Ϊ11m��
�����������⿼����ǽ�ֱ�������ε�Ӧ�é����Ǹ������⣬�������Ǹ��ǵĸ�����������Ǻ����Ķ����ǽ���Ĺؼ����ӳ�AD��BC���ӳ�����G����DH��BG��H�������Ǻ���������CH��DH�ij����ó�CG����AB=xm���������еĶ������BG���ó����̣��ⷽ�̼��ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��С�����ÿ���ʱ��������һ������ܣ�ͼ2�����Ľ���ͼ����ֱ���õ���������ӵĽ���ΪA��B��AB=40cm���������͵�C��AB�ľ���Ϊ10cm���������İ뾶Ϊcm��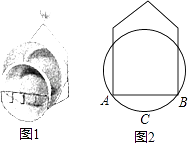
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�ڰ�����Ҫ�������ͼ����Ҫ��д������������ͼ�ۼ�����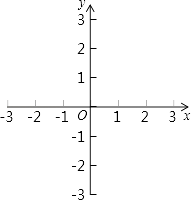
��1���ԣ�0��0��ΪԲ�ģ�3Ϊ�뾶��Բ��
��2���ԣ�0����1��ΪԲ�ģ�1Ϊ�뾶���»���Բ��
��3���ֱ��ԣ���1��1������1��1��ΪԲ�ģ�0.5Ϊ�뾶��Բ��
��4���ֱ��ԣ���1��1������1��1��ΪԲ�ģ�1Ϊ�뾶���ϻ���Բ��
�����ϡ�����ָ�ھ���Բ�ĵ�ˮƽ�ߵ��Ϸ����·���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C����ABΪֱ���ġ�O�ϣ�AD�����C�����ߴ�ֱ������Ϊ��D��AD����O�ڵ�E��
��1����֤��ACƽ�֡�DAB��
��2������BE��AC�ڵ�F����cos��CAD= ![]() ����
���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y1=ax+c�ͷ���������y2= ![]() ��ͼ����ͼ��ʾ������κ���y3=ax2+bx+c�Ĵ���ͼ���ǣ� ��
��ͼ����ͼ��ʾ������κ���y3=ax2+bx+c�Ĵ���ͼ���ǣ� �� 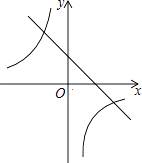
A.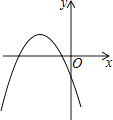
B.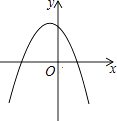
C.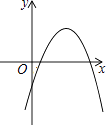
D.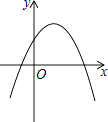
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���涨����a��b֮���һ�����㣬����(a��b)�����ac��b����ô(a��b)��c.���磺��23��8����(2��8)��3.
(1)���������涨����գ�(3��27)��________��(5��1)��________��![]() ��________��
��________��
(2)С�����о���������ʱ����һ������(3n��4n)��(3��4)��С�����������µ����ɣ�
��(3n��4n)��x����(3n)x��4n����(3x)n��4n��
��3x��4����(3��4)��x��
��(3n��4n)��(3��4)��
���㳢���������ַ����ж�(3��4)��(3��5)��(3��20)�Ƿ����������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a1= ![]() ��a2=
��a2= ![]() ��a3=
��a3= ![]() ������an+1=
������an+1= ![]() ��nΪ����������t��0��1������a2016=���ú���t�Ĵ���ʽ��ʾ����
��nΪ����������t��0��1������a2016=���ú���t�Ĵ���ʽ��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����B����C��AB��EF����˵����BGF����C�������ƽ�����̣�����������������Ӧ���������ݣ�
�⣺�ߡ�B����C������֪��
��AB���� �������� ����
��AB��EF������֪��
���� ������ �������� ����
���BGF����C������ ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ϧ��Ķ�������n���ε����ĵ�O�����Ϧ����Ŷ���O��ת���ǵ���������n�� �ε����߷ֱ��ڵ�M��N���Ϧ�����n�����ص��������ΪS��
��1����n=4���߳�Ϊ2���Ϧ�=90��ʱ����ͼ��1������ֱ��д��S��ֵ��
��2����n=5���Ϧ�=72��ʱ����ͼ��2������������ת�����У�S�Ƿ����仯����˵�����ɣ�
��3����n=6���Ϧ�=120��ʱ����ͼ��3���������S��ԭ������������ļ���֮��������˵�����ɣ������Ϧ���ƽ������BC�߽��ڵ�P���ж��ı���OMPN����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com