
|
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
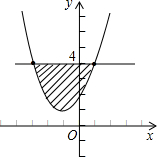 ��x��y��Ϊ���㣬�ú�����ͼ��Ϊ���������ߣ����磺y=x2+2x+2����
��x��y��Ϊ���㣬�ú�����ͼ��Ϊ���������ߣ����磺y=x2+2x+2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2012•��ƽ����ƽ��ֱ������ϵ�У�����OABC��ͼ��ʾ���ã���A��x���ϣ���B������Ϊ��m��1����m��0�������˾�����O����ʱ����ת90�㣬�õ�����OA��B��C�䣮
��2012•��ƽ����ƽ��ֱ������ϵ�У�����OABC��ͼ��ʾ���ã���A��x���ϣ���B������Ϊ��m��1����m��0�������˾�����O����ʱ����ת90�㣬�õ�����OA��B��C�䣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2009��㶫ʡï���и��н�ѧУ����������ѧ���� ���ͣ�059
��֪����ͼ��ֱ��l��![]() ��������
��������![]() ��һ�������ߵĶ���B1(1��y1)��B2(2��y2)��B3(3��y3)������Bn(n��yn)(nΪ������)������ֱ��l�ϵĵ㣬������������x��������Ľ��������ǣ�A1(x1��0)��A2(x2��0)��A3(x3��0)������An+1(xn+1��0)(nΪ������)����x1��d(0��d��1)��
��һ�������ߵĶ���B1(1��y1)��B2(2��y2)��B3(3��y3)������Bn(n��yn)(nΪ������)������ֱ��l�ϵĵ㣬������������x��������Ľ��������ǣ�A1(x1��0)��A2(x2��0)��A3(x3��0)������An+1(xn+1��0)(nΪ������)����x1��d(0��d��1)��
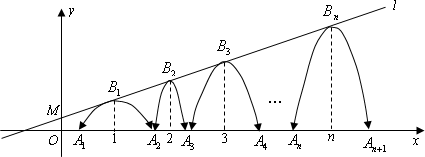
(1)��b��ֵ��
(2)����A1��B1��A2�������ߵĽ���ʽ(�ú�d�Ĵ���ʽ��ʾ)
(3)���壺�������ߵĶ�����x����������㹹�ɵ���������ֱ�������Σ������������߾ͳ�Ϊ������������������
̽������d(0��d��1)�Ĵ�С�仯ʱ���������������Ƿ���������������������ڣ����������Ӧ��d��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com