
 如图,一次函数y=kx+b的图象分别与反比例函数y=$\frac{a}{x}$的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB.
如图,一次函数y=kx+b的图象分别与反比例函数y=$\frac{a}{x}$的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB.分析 (1)利用待定系数法即可解答;
(2)设点M的坐标为(x,2x-5),根据MB=MC,得到∴$\sqrt{{x}^{2}{+(2x-10+10)}^{2}}$=$\sqrt{{x}^{2}{+(2x-10-10)}^{2}}$,即可解答.
解答 解:(1)把点A(8,6)代入函数y=$\frac{a}{x}$得:a=8×6=48,
∴y=$\frac{48}{x}$.
OA=$\sqrt{{8}^{2}{+6}^{2}}$=10,
∵OA=OB,
∴OB=10,
∴点B的坐标为(0,-10),
把B(0,-10),A(8,6)代入y=kx+b得:
$\left\{\begin{array}{l}{b=-10}\\{\;}\\{8k+b=6}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=2}\\{\;}\\{b=-10}\end{array}\right.$
∴y=2x-10;
(2)∵点M在一次函数y=2x-10上,
∴设点M的坐标为(x,2x-10),
∵MB=MC,
∴$\sqrt{{x}^{2}{+(2x-10+10)}^{2}}$=$\sqrt{{x}^{2}{+(2x-10-10)}^{2}}$
解得:x=5,
∴点M的坐标为(5,0).
点评 本题考查了一次函数与反比例函数的交点,解决本题的关键是利用待定系数法求解析式.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:填空题
 如图,已知抛物线y=-x2-2x+3与坐标轴分别交于A,B,C三点,在抛物线上找到一点D,使得∠DCB=∠ACO,则D点坐标为(-$\frac{5}{2}$,$\frac{7}{4}$)或(-4,-5).
如图,已知抛物线y=-x2-2x+3与坐标轴分别交于A,B,C三点,在抛物线上找到一点D,使得∠DCB=∠ACO,则D点坐标为(-$\frac{5}{2}$,$\frac{7}{4}$)或(-4,-5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 棉花纤维长度x | 频数 |
| 0≤x<8 | 1 |
| 8≤x<16 | 2 |
| 16≤x<24 | 8 |
| 24≤x<32 | 6 |
| 32≤x<40 | 3 |
| A. | 0.8 | B. | 0.7 | C. | 0.4 | D. | 0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
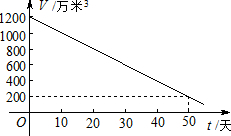 由于干旱,某水库的蓄水量随时间的增加而直线下降.若该水库的蓄水量V(万米3)与干旱的时间t(天)的关系如图所示,则下列说法正确的是( )
由于干旱,某水库的蓄水量随时间的增加而直线下降.若该水库的蓄水量V(万米3)与干旱的时间t(天)的关系如图所示,则下列说法正确的是( )| A. | 干旱第50天时,蓄水量为1200万米3 | |
| B. | 干旱开始后,蓄水量每天增加20万米3 | |
| C. | 干旱开始时,蓄水量为200万米3 | |
| D. | 干旱开始后,蓄水量每天减少20万米3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com