
【题目】如图,在平行四边形![]() 中,
中,![]() 是
是![]() 的中点,延长
的中点,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() .
.
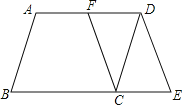
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由“平行四边形的对边平行且相等”的性质推知AD∥BC,且AD=BC;然后根据中点的定义、结合已知条件推知四边形CEDF的对边平行且相等(DF=CE,且DF∥CE),即四边形CEDF是平行四边形;
(2)如图,过点D作DH⊥BE于点H,构造含30度角的直角△DCH和直角△DHE.通过解直角△DCH和在直角△DHE中运用勾股定理来求线段ED的长度.
证明:(1)在ABCD中,AD∥BC,且AD=BC.
∵F是AD的中点,
∴DF=![]() AD.
AD.
又∵CE=![]() BC,
BC,
∴DF=CE,且DF∥CE,
∴四边形CEDF是平行四边形;
(2)解:如图,过点D作DH⊥BE于点H.
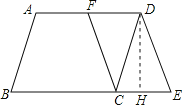
在ABCD中,∵∠B=60°,
∴∠DCE=60°.
∵AB=4,
∴CD=AB=4,
∴CH=![]() CD=2,DH=2
CD=2,DH=2![]() .
.
在CEDF中,CE=DF=![]() AD=3,则EH=1.
AD=3,则EH=1.
∴在Rt△DHE中,根据勾股定理知DE=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
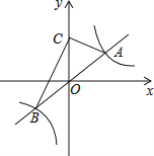
【题目】如图,反比例函数y=![]() (k>0)的图象与一次函数y=
(k>0)的图象与一次函数y=![]() x的图象交于A、B两点(点A在第一象限).
x的图象交于A、B两点(点A在第一象限).
(1)当点A的横坐标为4时.
①求k的值;
②根据反比例函数的图象,直接写出当-4<x<1(x≠0)时,y的取值范围;
(2)点C为y轴正半轴上一点,∠ACB=90°,且△ACB的面积为10,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
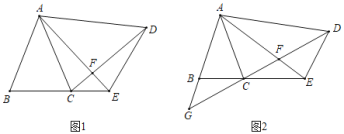
【题目】我们定义:如图1,在![]() 中,把AB绕点
中,把AB绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到
得到![]() ,把AC绕点
,把AC绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得到
得到![]() ,连接
,连接![]() .当
.当![]() 时,我们称
时,我们称![]() 是
是![]() 的“旋补三角形”,边
的“旋补三角形”,边![]() 上的中线AD叫做
上的中线AD叫做![]() 的“旋补中线”,点A叫做“旋补中心”.
的“旋补中线”,点A叫做“旋补中心”.
特例感知
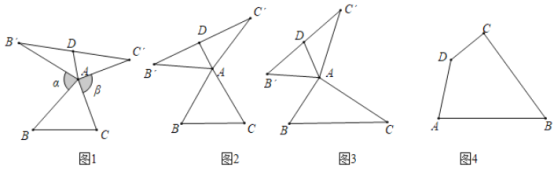
(1)在图2、图3中,![]() 是△ABC的“旋补三角形”,
是△ABC的“旋补三角形”,![]() 是的“旋补中线”.
是的“旋补中线”.
①如图2,当![]() 为等边三角形时,AD与
为等边三角形时,AD与![]() 的数量关系为AD=
的数量关系为AD= ![]() ;
;
②如图3,当![]() 时,则
时,则![]() 长为 .
长为 .
猜想论证
(2)在图1中,当![]() 为任意三角形时,猜想
为任意三角形时,猜想![]() 与BC的数量关系,并给予证明.
与BC的数量关系,并给予证明.
拓展应用
(3)如图4,在四边形![]() 中,
中,![]() .在四边形内部是否存在点
.在四边形内部是否存在点![]() ,使
,使![]() 是
是![]() 的“旋补三角形”?若存在,求
的“旋补三角形”?若存在,求![]() 的“旋补中线”长;若不存在,说明理由.
的“旋补中线”长;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
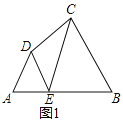
【题目】如图1,在△ABC和△ADE中,∠BAC=∠EAD,AB=AC,AD=AE,连接CD、AE交于点F.
(1)求证:BE=CD.
(2)当∠BAC=∠EAD=30°,AD⊥AB时(如图2),延长DC、AB交于点G,请直接写出图中除△ABC、△ADE以外的等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
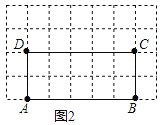
【题目】阅读理解:
如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
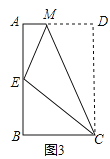
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种优质蜜柚,投入市场销售时,经调查,该蜜柚每天销售量y(千克)与销售单价x(元/千克)之间符合一次函数关系,如图所示.
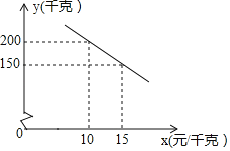
(1)求y与x的函数关系式;
(2)某农户今年共采摘该蜜柚4500千克,其保质期为40天,若以18元/千克销售,问能否在保质期内销售完这批蜜柚?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com