
分析 先算括号里面的,再算除法,最后把a=1代入进行计算即可.
解答 解:原式=[$\frac{a-1}{{(a-2)}^{2}}$-$\frac{a+2}{a(a-2)}$]÷$\frac{4-a}{a}$
=$\frac{{a}^{2}-a-{a}^{2}+4}{{a(a-2)}^{2}}$•$\frac{a}{4-a}$
=$\frac{4-a}{{a(a-2)}^{2}}$•$\frac{a}{4-a}$
=$\frac{1}{{(a-2)}^{2}}$,
当a=1时,原式=$\frac{1}{{(1-2)}^{2}}$=1.
点评 本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
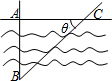 如图,为了测量河两岸A、B两点的距离,在与AB垂直的方向点C处测得AC=a,∠ACB=θ,那么AB等于( )
如图,为了测量河两岸A、B两点的距离,在与AB垂直的方向点C处测得AC=a,∠ACB=θ,那么AB等于( )| A. | a•sinθ | B. | a•tanθ | C. | a•cosθ | D. | $\frac{a}{tanθ}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
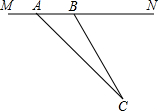 “为了安全,请勿超速”,如图所示是一条已经建成并通车的公路,且该公路的某直线路段MN上限速17m/s,为了检测来往车辆是否超速,交警在MN旁设立了观测点C.若某次从观测点C测得一汽车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200m.
“为了安全,请勿超速”,如图所示是一条已经建成并通车的公路,且该公路的某直线路段MN上限速17m/s,为了检测来往车辆是否超速,交警在MN旁设立了观测点C.若某次从观测点C测得一汽车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com