
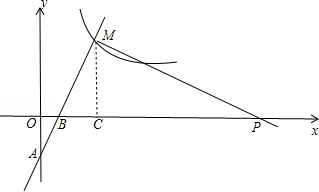
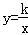 的图象在第一象限内的交点为M(3,m).
的图象在第一象限内的交点为M(3,m).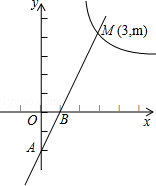
 (2)存在.理由见解析
(2)存在.理由见解析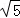 ;根据M点坐标得到MC=4,BC=2,则利用勾股定理可计算出BM=2
;根据M点坐标得到MC=4,BC=2,则利用勾股定理可计算出BM=2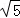 ,然后证明Rt△OBA∽Rt△MBP,利用相似比计算出BP,于是可确定P点坐标.
,然后证明Rt△OBA∽Rt△MBP,利用相似比计算出BP,于是可确定P点坐标. 得k=3×4=12,
得k=3×4=12, ;
; =
=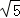 ,
,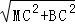 =2
=2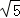 ,
,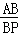 =
= ,即
,即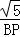 =
=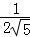 ,
,


科目:初中数学 来源:不详 题型:解答题
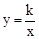 (k>0,x>0)与OA边交于点E,过点F作FC⊥x轴于点C,连结EF、OF.
(k>0,x>0)与OA边交于点E,过点F作FC⊥x轴于点C,连结EF、OF.
 ,求反比例函数的解析式;
,求反比例函数的解析式;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
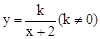 的图象是由反比例函数
的图象是由反比例函数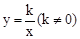 的图象向左平移2个单位长度得到.灵活运用这一知识解决问题.
的图象向左平移2个单位长度得到.灵活运用这一知识解决问题.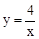 的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(2,2)和点B.
的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(2,2)和点B.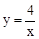 的图象和直线AB同时向右平移n(n>0)个单位长度,得到的图象分别记为C′和l′,已知图象C′经过点M(2,4).
的图象和直线AB同时向右平移n(n>0)个单位长度,得到的图象分别记为C′和l′,已知图象C′经过点M(2,4).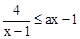 的解集.
的解集.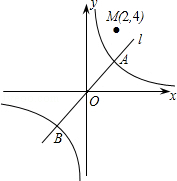
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
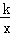 的图象在每一条曲线上,y都随x的增大而增大,
的图象在每一条曲线上,y都随x的增大而增大,查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 (k≠0,x>0)的图象经过OB的中点D,与BC边交于点E,点E的横坐标是4,则k的值是
(k≠0,x>0)的图象经过OB的中点D,与BC边交于点E,点E的横坐标是4,则k的值是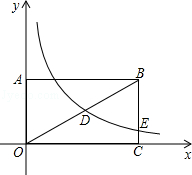
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ,下列说法正确的是
,下列说法正确的是| A.图象经过点(1,﹣3) | B.图象在第二、四象限 |
| C.x>0时,y随x的增大而增大 | D.x<0时,y随x增大而减小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com