
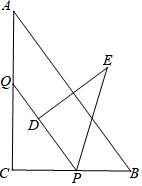
 如图,Rt△ABC中,∠C=90°,AB=5,BC=3,点P、Q分别在BC、AC上,CP=3x,CQ=4x (0<x<1),把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
如图,Rt△ABC中,∠C=90°,AB=5,BC=3,点P、Q分别在BC、AC上,CP=3x,CQ=4x (0<x<1),把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.分析 (1)根据勾股定理得到AC=4,根据旋转的性质得到DE=CQ=4x,DE⊥PQ,根据相似三角形的性质得到∠CPQ=∠B,推出PQ∥AB,于是得到结论;
(2)连接AD,根据PQ∥AB可知∠ADQ=∠DAB,再由点D在∠BAC的平分线上,得出∠DAQ=∠DAB,故∠ADQ=∠DAQ,AQ=DQ.在Rt△CPQ中根据勾股定理可知,AQ=12-4x,故可得出x的值,进而得出结论;
(3)分①当0<x≤$\frac{3}{8}$时,②当$\frac{3}{8}$<x<1时,两种情况进行分类讨论.
解答 解:(1)在Rt△ABC中,∠C=90°,AB=5,BC=3,
∴AC=4,
∵把△PCQ绕点P旋转,得到△PDE,
∴DE=CQ=4x,DE⊥PQ,
∵$\frac{PC}{BC}$=$\frac{3x}{3}$=x,$\frac{CQ}{AC}$=$\frac{4x}{4}$=x,
∴$\frac{PC}{BC}=\frac{CQ}{AC}$.
∵∠C=∠C,
∴△PQC∽△BAC,
∴∠CPQ=∠B,
∴PQ∥AB,
∴∠DPE=∠PGB.
∵∠CPQ=∠DPE,∠CPQ=∠B,
∴∠B=∠PGB,
∴PB=PG=5x,
∴3x+5x=3,
∴x=$\frac{3}{8}$,
故答案为:$\frac{3}{8}$;
(2)解:连接AD,
∵PQ∥AB,
∴∠ADQ=∠DAB.
∵点D在∠BAC的平分线上,
∴∠DAQ=∠DAB,
∴∠ADQ=∠DAQ,
∴AQ=DQ.
在Rt△CPQ中,PQ=5x,
∵PD=PC=3x,
∴DQ=2x.
∵AQ=4-4x,
∴4-4x=2x,解得x=$\frac{2}{3}$,
∴CP=3x=2;
(3)解:当点E在AB上时,
由(1)知,x=$\frac{3}{8}$.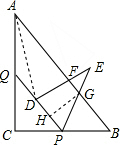
①当0<x≤$\frac{3}{8}$时,S=$\frac{1}{2}$CQ•CP=$\frac{1}{2}$•3x•4x=6x;
②当$\frac{3}{8}$<x<1时,设PE交AB于点G,DE交AB于F,作GH⊥PQ,垂足为H,
∴HG=DF,FG=DH,Rt△PHG∽Rt△PDE,
∴$\frac{GH}{ED}$=$\frac{PG}{PE}$=$\frac{PH}{PD}$.
∵PG=PB=9-3x,
∴$\frac{GH}{4x}$=$\frac{3-3x}{5x}$=$\frac{PH}{3x}$,
∴GH=$\frac{4}{5}$(3-3x),PH=$\frac{3}{5}$(3-3x),
∴FG=DH=3x-$\frac{3}{5}$(3-3x),
∴S=$\frac{1}{2}$(FG+PD)•HG=$\frac{1}{2}$[3x-$\frac{3}{5}$(3-3x)+3x]×$\frac{4}{5}$(3-3x)=-$\frac{234}{25}$x2+$\frac{36}{5}$x+$\frac{54}{25}$.
综上所述,S=$\left\{\begin{array}{l}{6x(0<x≤\frac{3}{8})}\\{-\frac{234}{25}{x}^{2}+\frac{36}{5}x+\frac{54}{25}(\frac{3}{8}<x<1)}\end{array}\right.$.
点评 本题考查的是几何变换综合题,涉及到勾股定理、相似三角形的判定与性质,角平分线,方程,一次函数等知识,在解答(3)时能正确进行分类讨论是解题的关键.


科目:初中数学 来源: 题型:选择题
 如图,△ABC的中线BD、CE交于点O,连接OA,点G、F分别为OC、OB的中点,BC=7,AO=5,则四边形DEFG的周长为( )
如图,△ABC的中线BD、CE交于点O,连接OA,点G、F分别为OC、OB的中点,BC=7,AO=5,则四边形DEFG的周长为( )| A. | 10 | B. | 12 | C. | 14 | D. | 24 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,DE∥BC,若AD=3,BD=4,BC=5,则DE的长为( )
如图,在△ABC中,DE∥BC,若AD=3,BD=4,BC=5,则DE的长为( )| A. | $\frac{15}{4}$ | B. | $\frac{15}{7}$ | C. | $\frac{12}{5}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
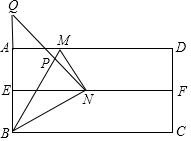 如图,四边形ABCD为矩形纸片,对折纸片,使得AD与BC重合,得到折痕EF,把纸片展平后,再把纸片沿着BM折叠,使得点A与EF上的点N重合,在折痕BM上取一点P,使得BP=BA,连接NP并延长.交BA的延长线于点Q.若AB=6.则AQ的长为3$\sqrt{3}$-3.
如图,四边形ABCD为矩形纸片,对折纸片,使得AD与BC重合,得到折痕EF,把纸片展平后,再把纸片沿着BM折叠,使得点A与EF上的点N重合,在折痕BM上取一点P,使得BP=BA,连接NP并延长.交BA的延长线于点Q.若AB=6.则AQ的长为3$\sqrt{3}$-3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
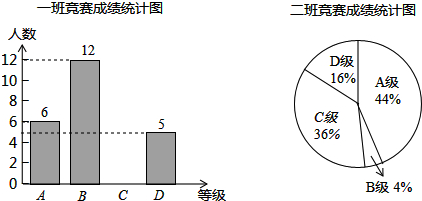
| 平均数(分) | 中位数(分) | 众数(分) | |
| 一班 | 87.6 | 90 | 90 |
| 二班 | 87.6 | 80 | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com