
【题目】如图,正方形ABCD中,点E,F分别在BC,CD上, ΔAEF是等边三角形,连接AC交EF于点G,下列结论:①CE=CF,②∠AEB=75°,③AG=2GC,④BE+DF=EF,⑤S△CEF=2S△ABE,其中结论正确的个数为( )
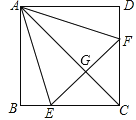
A. 2个 B. 3个 C. 4个 D. 5个
【答案】B
【解析】分析:本题是四边形的综合题,利用三角形的知识解决即可.
解析:∵四边形ABCD是正方形,∴AB=AD,∵△AEF是等边三角形,∴AE=AF,在Rt△ABE和Rt△ADF中,![]() ,∴Rt△ABE≌Rt△ADF(HL),∴BE=DF,∴①说法正确;∵BC=DC,∴BC-BE=CD-DF,∴CE=CF,∴△ECF是等腰直角三角形,∴∠CFE=45°∴∠AFD=75°∴∠DAF=15°∴②正确;∵AC是正方形ABCD的对角线,∴∠BCA=45°∴AC⊥EF又CE=CF∴AC垂直平分EF,∴③正确;在AD上取一点G,连接FG,使AG=GF,则∠DAF=∠GFA=15°,∴∠DGF=2∠DAF=30°,
,∴Rt△ABE≌Rt△ADF(HL),∴BE=DF,∴①说法正确;∵BC=DC,∴BC-BE=CD-DF,∴CE=CF,∴△ECF是等腰直角三角形,∴∠CFE=45°∴∠AFD=75°∴∠DAF=15°∴②正确;∵AC是正方形ABCD的对角线,∴∠BCA=45°∴AC⊥EF又CE=CF∴AC垂直平分EF,∴③正确;在AD上取一点G,连接FG,使AG=GF,则∠DAF=∠GFA=15°,∴∠DGF=2∠DAF=30°,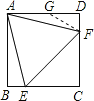
设DF=1,则AG=GF=2,DG=![]() ,∴AD=CD=2+
,∴AD=CD=2+![]() ,CF=CE=CD-DF=1+
,CF=CE=CD-DF=1+![]() ,∴EF=
,∴EF=![]() CF=
CF=![]() +
+![]() ,而BE+DF=2,∴④说法错误;
,而BE+DF=2,∴④说法错误;
∵S△ABE+SADF=2S△ABE=2×![]() AD×DF=2+
AD×DF=2+![]() ,
,
S△CEF=![]() CE×CF=
CE×CF=![]() ,∴⑤正确
,∴⑤正确
故选B.
定睛:本题考察的知识点为正方形的性质、全等三角形的判定与性质、等边三角形的性质.利用知识点逐个进行证明.


科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( ) 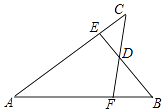
A.①
B.②
C.①和②
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分7分) 已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=![]() OB.
OB.
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个多项式加上3y2﹣2y﹣5得到多项式5y3﹣4y﹣6,则原来的多项式为( )
A.5y3+3y2+2y﹣1
B.5y3﹣3y2﹣2y﹣6
C.5y3+3y2﹣2y﹣1
D.5y3﹣3y2﹣2y﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)填空:点A坐标为 ;抛物线的解析式为 .
(2)在图1中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图2中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
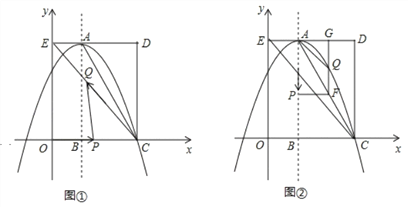
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】使(x2+px+8)(x2﹣3x+q)乘积中不含x2和x3项的p,q的值分别是( )
A.p=3,q=1
B.p=﹣3,q=﹣9
C.p=0,q=0
D.p=﹣3,q=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件发生的概率为0的是( )
A.射击运动员只射击1次,就命中靶心
B.任取一个实数x,都有|x|≥0
C.画一个三角形,使其三边的长分别为8cm,6cm,2cm
D.抛掷一枚质地均匀且六个面分别刻有1到6的点数的正方体骰子,朝上一面的点数为6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com